Regge theory
Encyclopedia
In quantum physics, Regge theory is the study of the analytic properties of scattering
as a function of angular momentum, where the angular momentum is not restricted to be an integer but is allowed to take any complex value
. The nonrelativistic theory was developed by Tullio Regge
in 1957.
of the scattering angle as a power that changes as the scattering energy changes:
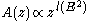
where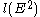
is the noninteger value of the angular momentum of a would-be bound state with energy 
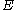. It is determined by solving the radial Schrödinger equation and it smoothly interpolates the energy of wavefunctions with different angular momentum but with the same radial excitation number. The trajectory function is a function of 
for relativistic generalization. The expression 
is known as the Regge trajectory function, and when it is an integer, the particles form an actual bound state with this angular momentum. The asymptotic form applies when 
much greater than one, which is not a physical limit in nonrelativistic scattering.
Shortly afterwards, Stanley Mandelstam
noted that in relativity the purely formal limit of
large is near to a physical limit — the limit of large 
. Large 
means large energy in the crossed channel, where one of the incoming particles has an energy momentum that makes it an energetic outgoing antiparticle. This observation turned Regge theory from a mathematical curiosity into a physical theory: it demands that the function that determines the falloff rate of the scattering amplitude for particle-particle scattering at large energies is the same as the function that determines the bound state energies for a particle-antiparticle system as a function of angular momentum.
The switch required swapping the Mandelstam variable
, which is the square of the energy, for 
, which is the squared momentum transfer, which for elastic soft collisions of identical particles is s times one minus the cosine of the scattering angle. The relation in the crossed channel becomes
...which says that the amplitude has a different power law falloff as a function of energy at different corresponding angles, where corresponding angles are those with the same value of
. It predicts that the function that determines the power law
is the same function that interpolates the energies where the resonances appear. The range of angles where scattering can be productively described by Regge theory shrinks into a narrow cone around the beam-line at large energies.
In 1960 Geoffrey Chew
and Steven Frautschi
conjectured from limited data that the strongly interacting particles had a very simple dependence of the squared-mass on the angular momentum: the particles fall into families where the Regge trajectory functions were straight lines:
with the same constant 
for all the trajectories. The straight-line Regge trajectories were later understood as arising from massless endpoints on rotating relativistic strings. Since a Regge description implied that the particles were bound states, Chew and Frautschi concluded that none of the strongly interacting particles were elementary.
Experimentally, the near-beam behavior of scattering did fall off with angle as explained by Regge theory, leading many to accept that the particles in the strong interactions were composite. Much of the scattering was diffractive, meaning that the particles hardly scatter at all — staying close to the beam line after the collision. Vladimir Gribov
noted that the Froissart bound combined with the assumption of maximum possible scattering implied there was a Regge trajectory that would lead to logarithmically rising cross sections, a trajectory nowadays known as the Pomeron
. He went on to formulate a quantitative perturbation theory for near beam line scattering dominated by multi-Pomeron exchange.
From the fundamental observation that hadrons are composite, there grew two points of view. Some correctly advocated that there were elementary particles, nowadays called quarks and gluons, which made a quantum field theory in which the hadrons were bound states. Others also correctly believed that it was possible to formulate a theory without elementary particles — where all the particles were bound states lying on Regge trajectories and scatter self-consistently. This was called S-matrix theory
.
The most successful S-matrix approach centered on the narrow-resonance approximation, the idea that there is a consistent expansion starting from stable particles on straight-line Regge trajectories. After many false starts, Dolen Horn and Schmidt understood a crucial property that led Gabriele Veneziano
to formulate a self-consistent scattering amplitude, the first string theory
. Mandelstam noted that the limit where the regge trajectories are straight is also the limit where the lifetime of the states is long.
As a fundamental theory of strong interaction
s at high energies, Regge theory enjoyed a period of interest in the 1960s, but it was largely succeeded by quantum chromodynamics
. As a phenomenological theory, it is still an indispensable tool for understanding near-beam line scattering and scattering at very large energies. Modern research focuses both on the connection to perturbation theory and to string theory.
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
as a function of angular momentum, where the angular momentum is not restricted to be an integer but is allowed to take any complex value
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. The nonrelativistic theory was developed by Tullio Regge
Tullio Regge
Tullio Regge is an Italian theoretical physicist. He obtained a degree in physics from the University of Turin in 1952, and a Ph.D. in physics from the University of Rochester in 1957 under the direction of Robert Marshak. From 1958 to 1959 Regge held a post at the Max Planck Institute for...
in 1957.
History and Implications
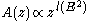
The main result of the theory is that the scattering amplitude for potential scattering grows as a function of the cosine of the scattering angle as a power that changes as the scattering energy changes:where
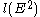is the noninteger value of the angular momentum of a would-be bound state with energy 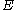. It is determined by solving the radial Schrödinger equation and it smoothly interpolates the energy of wavefunctions with different angular momentum but with the same radial excitation number. The trajectory function is a function of for relativistic generalization. The expression is known as the Regge trajectory function, and when it is an integer, the particles form an actual bound state with this angular momentum. The asymptotic form applies when much greater than one, which is not a physical limit in nonrelativistic scattering.Shortly afterwards, Stanley Mandelstam
Stanley Mandelstam
Stanley Mandelstam is a South African-born theoretical physicist. He introduced the relativistically invariant Mandelstam variables into particle physics in 1958 as a convenient coordinate system for formulating his double dispersion relations...
noted that in relativity the purely formal limit of
large is near to a physical limit — the limit of large . Large means large energy in the crossed channel, where one of the incoming particles has an energy momentum that makes it an energetic outgoing antiparticle. This observation turned Regge theory from a mathematical curiosity into a physical theory: it demands that the function that determines the falloff rate of the scattering amplitude for particle-particle scattering at large energies is the same as the function that determines the bound state energies for a particle-antiparticle system as a function of angular momentum.The switch required swapping the Mandelstam variable
Mandelstam variables
In theoretical physics, the Mandelstam variables are numerical quantities that encode the energy, momentum, and angles of particles in a scattering process in a Lorentz-invariant fashion...
, which is the square of the energy, for , which is the squared momentum transfer, which for elastic soft collisions of identical particles is s times one minus the cosine of the scattering angle. The relation in the crossed channel becomes...which says that the amplitude has a different power law falloff as a function of energy at different corresponding angles, where corresponding angles are those with the same value of
. It predicts that the function that determines the power lawPower law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
is the same function that interpolates the energies where the resonances appear. The range of angles where scattering can be productively described by Regge theory shrinks into a narrow cone around the beam-line at large energies.
In 1960 Geoffrey Chew
Geoffrey Chew
Geoffrey F. Chew is an American theoretical physicist.He has worked as a professor of physics at the UC Berkeley since 1957 and has been an emeritus since 1991. Chew holds a PhD in theoretical particle physics from the University of Chicago. Between 1950 and 1956, he was a physics faculty member...
and Steven Frautschi
Steven Frautschi
Steven Frautschi is an American theoretical physicist, Professor of Physics at the California Institute of Technology. He is known for his contributions to the bootstrap theory of the strong interactions....
conjectured from limited data that the strongly interacting particles had a very simple dependence of the squared-mass on the angular momentum: the particles fall into families where the Regge trajectory functions were straight lines:
with the same constant for all the trajectories. The straight-line Regge trajectories were later understood as arising from massless endpoints on rotating relativistic strings. Since a Regge description implied that the particles were bound states, Chew and Frautschi concluded that none of the strongly interacting particles were elementary.Experimentally, the near-beam behavior of scattering did fall off with angle as explained by Regge theory, leading many to accept that the particles in the strong interactions were composite. Much of the scattering was diffractive, meaning that the particles hardly scatter at all — staying close to the beam line after the collision. Vladimir Gribov
Vladimir Gribov
Vladimir Naumovich Gribov was a prominent Russian theoretical physicist, who worked on high-energy physics, quantum field theory and the Regge theory of the strong interactions.His best known contributions are the pomeron, the DGLAP equations, and the Gribov copies.-Life:Gribov completed his...
noted that the Froissart bound combined with the assumption of maximum possible scattering implied there was a Regge trajectory that would lead to logarithmically rising cross sections, a trajectory nowadays known as the Pomeron
Pomeron
In physics, the pomeron is a Regge trajectory, a family of particles with increasing spin, postulated in 1961 to explain the slowly rising cross section of hadronic collisions at high energies.-Overview:...
. He went on to formulate a quantitative perturbation theory for near beam line scattering dominated by multi-Pomeron exchange.
From the fundamental observation that hadrons are composite, there grew two points of view. Some correctly advocated that there were elementary particles, nowadays called quarks and gluons, which made a quantum field theory in which the hadrons were bound states. Others also correctly believed that it was possible to formulate a theory without elementary particles — where all the particles were bound states lying on Regge trajectories and scatter self-consistently. This was called S-matrix theory
S-matrix theory
S-matrix theory was a proposal for replacing local quantum field theory as the basic principle of elementary particle physics.It avoided the notion of space and time by replacing it with abstract mathematical properties of the S-matrix...
.
The most successful S-matrix approach centered on the narrow-resonance approximation, the idea that there is a consistent expansion starting from stable particles on straight-line Regge trajectories. After many false starts, Dolen Horn and Schmidt understood a crucial property that led Gabriele Veneziano
Gabriele Veneziano
Gabriele Veneziano, born in Florence, Italy), is an Italian theoretical physicist and the founder of string theory. . Has spent most of his scientific activities at CERN in Geneva, Switzerland...
to formulate a self-consistent scattering amplitude, the first string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. Mandelstam noted that the limit where the regge trajectories are straight is also the limit where the lifetime of the states is long.
As a fundamental theory of strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
s at high energies, Regge theory enjoyed a period of interest in the 1960s, but it was largely succeeded by quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. As a phenomenological theory, it is still an indispensable tool for understanding near-beam line scattering and scattering at very large energies. Modern research focuses both on the connection to perturbation theory and to string theory.