Recursive least squares filter
Encyclopedia
The Recursive least squares (RLS) adaptive filter
is an algorithm
which recursively finds the filter coefficients that minimize a weighted linear least squares
cost function relating to the input signals. This is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic
, while for the LMS and similar algorithm they are considered stochastic
. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity, and potentially poor tracking performance when the filter to be estimated (the "true system") changes.
s. For example, suppose that a signal d(n) is transmitted over an echoey, noisy channel that causes it to be received as
where
represents additive noise. We will attempt to recover the desired signal 
by use of a 
-tap FIR
filter,
:
where
is the vector containing the 
most recent samples of 
. Our goal is to estimate the parameters of the filter 
, and at each time n we refer to the new least squares estimate by 
. As time evolves, we would like to avoid completely redoing the least squares algorithm to find the new estimate for 
, in terms of 
.
The benefit of the RLS algorithm is that there is no need to invert matrices, thereby saving computational power. Another advantage is that it provides intuition behind such results as the Kalman filter
.
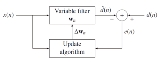
by appropriately selecting the filter coefficients 
, updating the filter as new data arrives. The error signal 
and desired signal 
are defined in the negative feedback
diagram below:
The error implicitly depends on the filter coefficients through the estimate
:
The weighted least squares error function
—the cost function we desire to minimize—being a function of e(n) is therefore also dependent on the filter coefficients:
where
is the "forgetting factor" which gives exponentially less weight to older error samples.
The cost function is minimized by taking the partial derivatives for all entries
of the coefficient vector 
and setting the results to zero
Next, replace
with the definition of the error signal
Rearranging the equation yields
This form can be expressed in terms of matrices
where
is the weighted sample correlation
matrix for
, and 
is the equivalent estimate for the cross-correlation
between
and 
. Based on this expression we find the coefficients which minimize the cost function as
This is the main result of the discussion.
Choosing
The smaller 
is, the smaller contribution of previous samples. This makes the filter more sensitive to recent samples, which means more fluctuations in the filter co-efficients. The 
case is referred to as the growing window RLS algorithm.
where
is a correction factor at time 
. We start the derivation of the recursive algorithm by expressing the cross correlation 
in terms of 
where
is the 
dimensional data vector
Similarly we express
in terms of 
by
In order to generate the coefficient vector we are interested in the inverse of the deterministic autocorrelation matrix. For that task the Woodbury matrix identity
comes in handy. With
The Woodbury matrix identity follows
To come in line with the standard literature, we define
where the gain vector
is
Before we move on, it is necessary to bring
into another form
Subtracting the second term on the left side yields
With the recursive definition of
the desired form follows
Now we are ready to complete the recursion. As discussed
The second step follows from the recursive definition of
. Next we incorporate the recursive definition of 
together with the alternate form of 
and get
With
we arrive at the update equation
where
is the a priori error. Compare this with the a posteriori
error; the error calculated after the filter is updated:
That means we found the correction factor
This intuitively satisfying result indicates that the correction factor is directly proportional to both the error and the gain vector, which controls how much sensitivity is desired, through the weighting factor,
.
Note that the recursion for
follows a Riccati equation
and thus draws parallels to the Kalman filter
.
Adaptive filter
An adaptive filter is a filter that self-adjusts its transfer function according to an optimization algorithm driven by an error signal. Because of the complexity of the optimization algorithms, most adaptive filters are digital filters. By way of contrast, a non-adaptive filter has a static...
is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which recursively finds the filter coefficients that minimize a weighted linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
cost function relating to the input signals. This is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic
Deterministic system (mathematics)
In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
, while for the LMS and similar algorithm they are considered stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity, and potentially poor tracking performance when the filter to be estimated (the "true system") changes.
Motivation
In general, the RLS can be used to solve any problem that can be solved by adaptive filterAdaptive filter
An adaptive filter is a filter that self-adjusts its transfer function according to an optimization algorithm driven by an error signal. Because of the complexity of the optimization algorithms, most adaptive filters are digital filters. By way of contrast, a non-adaptive filter has a static...
s. For example, suppose that a signal d(n) is transmitted over an echoey, noisy channel that causes it to be received as
where
represents additive noise. We will attempt to recover the desired signal by use of a -tap FIRFinite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filter,
:where
is the vector containing the most recent samples of . Our goal is to estimate the parameters of the filter , and at each time n we refer to the new least squares estimate by . As time evolves, we would like to avoid completely redoing the least squares algorithm to find the new estimate for , in terms of .The benefit of the RLS algorithm is that there is no need to invert matrices, thereby saving computational power. Another advantage is that it provides intuition behind such results as the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
.
Discussion
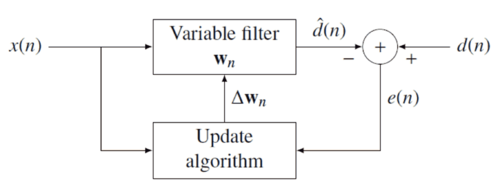
The idea behind RLS filters is to minimize a cost function by appropriately selecting the filter coefficients , updating the filter as new data arrives. The error signal and desired signal are defined in the negative feedbackNegative feedback
Negative feedback occurs when the output of a system acts to oppose changes to the input of the system, with the result that the changes are attenuated. If the overall feedback of the system is negative, then the system will tend to be stable.- Overview :...
diagram below:
The error implicitly depends on the filter coefficients through the estimate
:The weighted least squares error function
—the cost function we desire to minimize—being a function of e(n) is therefore also dependent on the filter coefficients:where
is the "forgetting factor" which gives exponentially less weight to older error samples.The cost function is minimized by taking the partial derivatives for all entries
of the coefficient vector and setting the results to zeroNext, replace
with the definition of the error signalRearranging the equation yields
This form can be expressed in terms of matrices
where
is the weighted sample correlationSample mean and sample covariance
The sample mean or empirical mean and the sample covariance are statistics computed from a collection of data on one or more random variables. The sample mean is a vector each of whose elements is the sample mean of one of the random variables that is, each of whose elements is the average of the...
matrix for
, and is the equivalent estimate for the cross-correlationCross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
between
and . Based on this expression we find the coefficients which minimize the cost function asThis is the main result of the discussion.
Choosing 
The smaller is, the smaller contribution of previous samples. This makes the filter more sensitive to recent samples, which means more fluctuations in the filter co-efficients. The case is referred to as the growing window RLS algorithm.Recursive algorithm
The discussion resulted in a single equation to determine a coefficient vector which minimizes the cost function. In this section we want to derive a recursive solution of the formwhere
is a correction factor at time . We start the derivation of the recursive algorithm by expressing the cross correlation in terms of
 |
 |
 |
|
 |
where
is the dimensional data vectorSimilarly we express
in terms of by
 |
 |
 |
In order to generate the coefficient vector we are interested in the inverse of the deterministic autocorrelation matrix. For that task the Woodbury matrix identity
Woodbury matrix identity
In mathematics , the Woodbury matrix identity, named after Max A. Woodbury says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix...
comes in handy. With
 |
 is  -by- |
 |
 is  -by-1 |
 |
 is 1-by- |
 |
 is the 1-by-1 identity matrixIdentity matrix In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context... |
The Woodbury matrix identity follows
 |
 |
 |
 |
 |
|
 |
||
 |
To come in line with the standard literature, we define
 |
 |
 |
where the gain vector
is
 |
 |
 |
Before we move on, it is necessary to bring
into another form
 |
 |
 |
 |
Subtracting the second term on the left side yields
 |
 |
 |
With the recursive definition of
the desired form followsNow we are ready to complete the recursion. As discussed
 |
 |
 |
The second step follows from the recursive definition of
. Next we incorporate the recursive definition of together with the alternate form of and get
 |
 |
 |
|
 |
With
we arrive at the update equation
 |
 |
 |
where
is the a priori error. Compare this with the a posteriori
A Posteriori
Apart from the album, some additional remixes were released exclusively through the iTunes Store. They are:*"Eppur si muove" – 6:39*"Dreaming of Andromeda" Apart from the album, some additional remixes were released exclusively through the iTunes Store. They are:*"Eppur si muove" (Tocadisco...
error; the error calculated after the filter is updated:
That means we found the correction factor
This intuitively satisfying result indicates that the correction factor is directly proportional to both the error and the gain vector, which controls how much sensitivity is desired, through the weighting factor,
.RLS algorithm summary
The RLS algorithm for a p-th order RLS filter can be summarized as| Parameters: |  filter order |
 forgetting factor |
|
 value to initialize  |
|
| Initialization: |  , |
 , |
|
 where  is the identity matrixIdentity matrix In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context... of rank  |
|
| Computation: | For  |
| |
|
| |
|
| |
|
| |
|
| . |
Note that the recursion for
follows a Riccati equationRiccati equation
In mathematics, a Riccati equation is any ordinary differential equation that is quadratic in the unknown function. In other words, it is an equation of the form y' = q_0 + q_1 \, y + q_2 \, y^2...
and thus draws parallels to the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
.
See also
- Adaptive filterAdaptive filterAn adaptive filter is a filter that self-adjusts its transfer function according to an optimization algorithm driven by an error signal. Because of the complexity of the optimization algorithms, most adaptive filters are digital filters. By way of contrast, a non-adaptive filter has a static...
- Kernel adaptive filterKernel adaptive filterKernel adaptive filtering is an adaptive filtering technique for general nonlinear problems. It is a natural generalization of linear adaptive filtering in reproducing kernel Hilbert spaces. Kernel adaptive filters are online kernel methods, closely related to some artificial neural networks such...
- Least mean squares filterLeast mean squares filterLeast mean squares algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean squares of the error signal . It is a stochastic gradient descent method in that the filter is only adapted based on the error at...
- Real-Time Outbreak and Disease SurveillanceReal-Time Outbreak and Disease SurveillanceReal-time outbreak and disease surveillance system is a biosurveillance system developed by the University of Pittsburgh, Department of Biomedical Informatics...
(RODS)