Rational sieve
Encyclopedia
In mathematics
, the rational sieve is a general algorithm
for factoring integers into prime factors
. It is essentially a special case of the general number field sieve
, and while it is far less efficient
than the general algorithm, it is conceptually far simpler. So while it is rather useless as a practical factoring algorithm, it is a helpful first step for those trying to understand how the general number field sieve works.
n. We choose a bound B, and identify the factor base
(which we will call P), the set of all primes less than or equal to B. Next, we search for positive integers z such that both z and z+n are B-smooth
— i.e. all of their prime factors are in P. We can therefore write, for suitable exponents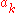
,
and likewise, for suitable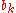
, we have
.
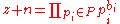But
and 
are congruent modulo 
, and so each such integer z that we find yields a multiplicative relation (mod n)
among the elements of P, i.e.
(where the ai and bi are nonnegative integers.)
When we have generated enough of these relations (it's generally sufficient that the number of relations be a few more than the size of P), we can use the methods of linear algebra
to multiply together these various relations in such a way that the exponents of the primes are all even. This will give us a congruence of squares
of the form a2≡b2 (mod n), which can be turned into a factorization of n, n = gcd
(a-b,n)×gcd(a+b,n). This factorization might turn out to be trivial (i.e. n=n×1), in which case we have to try again with a different combination of relations; but with luck we will get a nontrivial pair of factors of n, and the algorithm will terminate.
There are now several essentially different ways to combine these and end up with even exponents. For example,
Alternatively, equation (3) is in the proper form already:
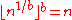holds for any 1 < b < log(n) using an integer version of Newton's method
for the root extraction.
The biggest problem is finding a sufficient number of z such that both z and z+n are B-smooth. For any given B, the proportion of numbers that are B-smooth decreases rapidly with the size of the number. So if n is large (say, a hundred digits), it will be difficult or impossible to find enough z for the algorithm to work. The advantage of the general number field sieve is that one need only search for smooth numbers of order n1/d for some positive integer d (typically 3 or 5), rather than of order n as required here.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rational sieve is a general algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for factoring integers into prime factors
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
. It is essentially a special case of the general number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
, and while it is far less efficient
Algorithmic efficiency
In computer science, efficiency is used to describe properties of an algorithm relating to how much of various types of resources it consumes. Algorithmic efficiency can be thought of as analogous to engineering productivity for a repeating or continuous process, where the goal is to reduce...
than the general algorithm, it is conceptually far simpler. So while it is rather useless as a practical factoring algorithm, it is a helpful first step for those trying to understand how the general number field sieve works.
Method
Suppose we are trying to factor the composite numberComposite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
n. We choose a bound B, and identify the factor base
Factor base
In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.-Usage:...
(which we will call P), the set of all primes less than or equal to B. Next, we search for positive integers z such that both z and z+n are B-smooth
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
— i.e. all of their prime factors are in P. We can therefore write, for suitable exponents
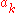,and likewise, for suitable
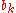, we have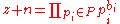.But
and are congruent modulo , and so each such integer z that we find yields a multiplicative relation (mod n)Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
among the elements of P, i.e.
(where the ai and bi are nonnegative integers.)
When we have generated enough of these relations (it's generally sufficient that the number of relations be a few more than the size of P), we can use the methods of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
to multiply together these various relations in such a way that the exponents of the primes are all even. This will give us a congruence of squares
Congruence of squares
In number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.-Derivation:Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality...
of the form a2≡b2 (mod n), which can be turned into a factorization of n, n = gcd
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(a-b,n)×gcd(a+b,n). This factorization might turn out to be trivial (i.e. n=n×1), in which case we have to try again with a different combination of relations; but with luck we will get a nontrivial pair of factors of n, and the algorithm will terminate.
Example
We will factor the integer n = 187 using the rational sieve. We'll arbitrarily try the value B=7, giving the factor base P = {2,3,5,7}. The first step is to test n for divisibility by each of the members of P; clearly if n is divisible by one of these primes, then we are finished already. However, 187 is not divisible by 2, 3, 5, or 7. Next, we search for suitable values of z; the first few are 2, 5, 9, and 56. The four suitable values of z give four multiplicative relations (mod 187):- 21305070 = 2 ≡ 189 = 20335071.............(1)
- 20305170 = 5 ≡ 192 = 26315070.............(2)
- 20325070 = 9 ≡ 196 = 22305072.............(3)
- 23305071 = 56 ≡ 243 = 20355070.............(4)
There are now several essentially different ways to combine these and end up with even exponents. For example,
- (1)×(4): After multiplying these and canceling out the common factor of 7 (which we can do since 7, being a member of P, has already been determined to be coprime with n), this reduces to 24 ≡ 38, or 42 ≡ 812. The resulting factorization is 187 = gcd(81-4,187) × gcd(81+4,187) = 11×17.
Alternatively, equation (3) is in the proper form already:
- (3): This says 32 ≡ 142 (mod n), which gives the factorization 187 = gcd(14-3,187) × gcd(14+3,187) = 11×17.
Limitations of the algorithm
The rational sieve, like the general number field sieve, cannot factor numbers of the form pm, where p is a prime and m is an integer. This is not a huge problem, though—such numbers are statistically rare, and moreover there is a simple and fast process to check whether a given number is of this form. Probably the most elegant method is to check whether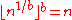 holds for any 1 < b < log(n) using an integer version of Newton's methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
for the root extraction.
The biggest problem is finding a sufficient number of z such that both z and z+n are B-smooth. For any given B, the proportion of numbers that are B-smooth decreases rapidly with the size of the number. So if n is large (say, a hundred digits), it will be difficult or impossible to find enough z for the algorithm to work. The advantage of the general number field sieve is that one need only search for smooth numbers of order n1/d for some positive integer d (typically 3 or 5), rather than of order n as required here.