
which provides the theoretical foundations for lossy data compression
; it addresses the problem of determining the minimal amount of entropy
(or information
) R that should be communicated over a channel, so that the source (input signal) can be approximately reconstructed at the receiver (output signal) without exceeding a given distortion D.
Introduction
Rate–distortion theory gives theoretical bounds for how much compression can be achieved using lossy compression methods. Many of the existing audio, speech, image, and video compression techniques have transforms, quantization, and bit-rate allocation procedures that capitalize on the general shape of rate–distortion functions.Rate–distortion theory was created by Claude Shannon in his foundational work on information theory.
In rate–distortion theory, the rate is usually understood as the number of bit
s per data sample to be stored or transmitted. The notion of distortion is a subject of on-going discussion. In the most simple case (which is actually used in most cases), the distortion is defined as the variance of the difference between input and output signal (i.e., the mean squared error
of the difference). However, since we know that most lossy compression techniques operate on data that will be perceived by human consumers (listening to music, watching pictures and video) the distortion measure should preferably be modeled on human perception
and perhaps aesthetics
: much like the use of probability
in lossless compression, distortion measures can ultimately be identified with loss function
s as used in Bayesian estimation
and decision theory
. In audio compression, perceptual models (and therefore perceptual distortion measures) are relatively well developed and routinely used in compression techniques such as MP3
or Vorbis
, but are often not easy to include in rate–distortion theory. In image and video compression, the human perception models are less well developed and inclusion is mostly limited to the JPEG
and MPEG weighting (quantization
, normalization
) matrix.
Rate–distortion functions
The functions that relate the rate and distortion are found as the solution of the following minimization problem: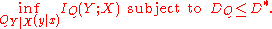
Here QY | X(y | x), sometimes called a test channel, is the conditional
probability density function
(PDF) of the communication channel output (compressed signal) Y for a given input (original signal) X, and IQ(Y ; X) is the mutual information
between Y and X defined as
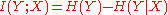
where H(Y) and H(Y | X) are the entropy of the output signal Y and the conditional entropy
of the output signal given the input signal, respectively:


The problem can also be formulated as a distortion–rate function, where we find the infimum over achievable distortions for given rate constraint. The relevant expression is:

The two formulations lead to functions which are inverses of each other.
The mutual information can be understood as a measure for prior uncertainty the receiver has about the sender's signal (H(Y)), diminished by the uncertainty that is left after receiving information about the sender's signal (H(Y | X)). Of course the decrease in uncertainty is due to the communicated amount of information, which is I(Y; X).
As an example, in case there is no communication at all, then H(Y |X) = H(Y) and I(Y; X) = 0. Alternatively, if the communication channel is perfect and the received signal Y is identical to the signal X at the sender, then H(Y | X) = 0 and I(Y; X) = H(Y) = H(X).
In the definition of the rate–distortion function, DQ and D* are the distortion between X and Y for a given QY | X(y | x) and the prescribed maximum distortion, respectively. When we use the mean squared error
as distortion measure, we have (for amplitude-continuous signals):

As the above equations show, calculating a rate–distortion function requires the stochastic description of the input X in terms of the PDF PX(x), and then aims at finding the conditional PDF QY | X(y | x) that minimize rate for a given distortion D*. These definitions can be formulated measure-theoretically to account for discrete and mixed random variables as well.
An analytical
solution to this minimization problem
is often difficult to obtain except in some instances for which we next offer two of the best known examples. The rate–distortion function of any source is known to obey several fundamental properties, the most important ones being that it is a continuous
, monotonically decreasing convex
(U) function
and thus the shape for the function in the examples is typical (even measured rate–distortion functions in real life tend to have very similar forms).
Although analytical solutions to this problem are scarce, there are upper and lower bounds to these functions including the famous Shannon lower bound (SLB), which in the case of squared error and memoryless sources, states that for arbitrary sources with finite differential entropy,

where h(D) is the differential entropy of a Gaussian random variable with variance D. This lower bound is extensible to sources with memory and other distortion measures. One important feature of the SLB is that it is asymptotically tight in the low distortion regime for a wide class of sources and in some occasions, it actually coincides with the rate–distortion function. Shannon Lower Bounds can generally be found if the distortion between any two numbers can be expressed as a function of the difference between the value of these two numbers.
The Blahut-Arimoto algorithm, co-invented by Richard Blahut
, is an elegant iterative technique for numerically obtaining rate–distortion functions of arbitrary finite input/output alphabet sources and much work has been done to extend it to more general problem instances.
Memoryless (independent) Gaussian source
If we assume that PX(x) is Gaussian with varianceσ2, and if we assume that successive samples of the signal X are stochastically independent (or, if you like, the source is memoryless
, or the signal is uncorrelated), we find the following analytical expression
for the rate–distortion function:
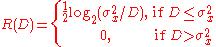
The following figure shows what this function looks like:
Rate–distortion theory tell us that no compression system exists that performs outside the gray area. The closer a practical compression system is to the red (lower) bound, the better it performs. As a general rule, this bound can only be attained by increasing the coding block length parameter. Nevertheless, even at unit blocklengths one can often find good (scalar) quantizers that operate at distances from the rate–distortion function that are practically relevant.
This rate–distortion function holds only for Gaussian memoryless sources. It is known that the Gaussian source is the most "difficult" source to encode: for a given mean square error, it requires the greatest number of bits. The performance of a practical compression system working on—say—images, may well be below the R(D) lower bound shown.
See also
- DecorrelationDecorrelationDecorrelation is a general term for any process that is used to reduce autocorrelation within a signal, or cross-correlation within a set of signals, while preserving other aspects of the signal. A frequently used method of decorrelation is the use of a matched linear filter to reduce the...
- Rate–distortion optimizationRate–distortion optimizationRate–distortion optimization is a method of improving video quality in video compression. The name refers to the optimization of the amount of distortion against the amount of data required to encode the video, the rate...
- Source codingSource codingIn information theory, Shannon's source coding theorem establishes the limits to possible data compression, and the operational meaning of the Shannon entropy....
- WhiteningWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...

