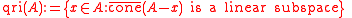Quasi-relative interior - AbsoluteAstronomy.com

In topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, a branch of mathematics, the quasi-relative interior of a subset of a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

is a refinement of the concept of the interior

Interior (topology)

In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....

. Formally, if

is a linear space then the algebraic interior of

where

denotes the closure

Closure

Closure may refer to:* Closure used to seal a bottle, jug, jar, can, or other container** Closure , a stopper* Closure , the process by which an organization ceases operations...

of the conic hull.

Let

is a normed vector space, if

is a convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

finite dimensional set then

such that

is the relative interior

Relative interior

In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.