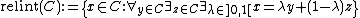Relative interior
Encyclopedia
In mathematics
, the relative interior of a set is a refinement of the concept of the interior
, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces. Intuitively, the relative interior of a set contains all points which are not on the "edge" of the set, relative to the smallest subspace in which this set lies.
Formally, the relative interior of a set S (denoted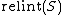
) is defined as its interior
within the affine hull
of S. In other words,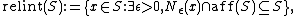
where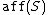
is the affine hull of S, and 
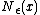is a ball
of radius
centered on 
. Any metric can be used for the construction of the ball; all metrics define the same set as the relative interior.
For convex sets C the relative interior can be defined: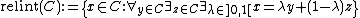
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the relative interior of a set is a refinement of the concept of the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces. Intuitively, the relative interior of a set contains all points which are not on the "edge" of the set, relative to the smallest subspace in which this set lies.
Formally, the relative interior of a set S (denoted
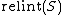) is defined as its interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
within the affine hull
Affine hull
In mathematics, the affine hull of a set S in Euclidean space Rn is the smallest affine set containing S, or equivalently, the intersection of all affine sets containing S...
of S. In other words,
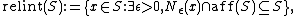
where
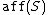is the affine hull of S, and 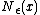is a ballBall (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
of radius
centered on . Any metric can be used for the construction of the ball; all metrics define the same set as the relative interior.For convex sets C the relative interior can be defined: