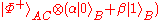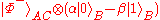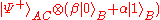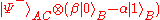Quantum teleportation
Encyclopedia
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit
(the basic unit of quantum information) can be transmitted exactly (in principle) from one location to another, without the qubit being transmitted through the intervening space. It is useful for quantum information processing
, however it does not immediately transmit classical information, and therefore cannot be used for communication
at superluminal (faster than light) speed. Quantum teleportation is unrelated to the common term teleportation - it does not transport the system itself, and does not concern rearranging particles to copy the form of an object.
The seminal paper first expounding the idea was published by Charles Bennett
and coauthors in 1993. It was first confirmed experimentally in 1997 by a group in Innsbruck
and has subsequently been shown to work over distances of up to 16 kilometers.
EPR pair
of qubits, performing a Bell measurement on the EPR pair, and manipulating the quantum state of one of the pair. The protocol is then as follows:
1. An EPR pair is generated and distributed to two separate locations, A and B.
2. At location A, a Bell measurement of the EPR pair qubit and the qubit to be teleported (for example, quantum state
of a photon) is performed, yielding two classical bits of information. Both qubits are destroyed.
3. Using the classical channel, the two bits are sent from A to B. (This is the only potentially time-consuming step, due to speed-of-light considerations.)
4. At location B, the EPR pair qubit is modified (if necessary), using the two bits to select the correct one of four possible quantum states. A qubit identical to that chosen for teleportation (for example, quantum state
of a photon) results.
. The longest distance yet claimed to be achieved for quantum teleportation is 16 km (9.9 mi) in May 2010 by Chinese scientists over free-space with an average of 89% accuracy.
In April 2011, experimenters reported that they had demonstrated teleportation of wave packets of light up to a bandwidth of 10 MHz while preserving strongly nonclassical superposition states.
has a qubit
in some arbitrary quantum state
. (A qubit may be represented as a superposition
of states, labeled
and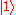 
.) Assume that this quantum state is not known to Alice and she would like to send this state to Bob. Ostensibly, Alice has the following options:
Option 1 is highly undesirable because quantum states are fragile and any perturbation en route would corrupt the state.
Option 2 is forbidden by the no-broadcast theorem
.
Option 3 (classical teleportation) has also been formally shown to be impossible. (See the no teleportation theorem
.) This is another way to say that quantum information cannot be measured reliably.
Thus, Alice seems to face an impossible problem. A solution was discovered by Bennett, et al. The components of a maximally entangled two-qubit state are distributed to Alice and Bob. The protocol then involves Alice and Bob interacting locally with the qubit(s) in their possession and Alice sending two classical bits to Bob. In the end, the qubit in Bob's possession will be in the desired state.
Alice applies a unitary operation on the qubits ac and measures the result to obtain two classical bits. In this process, the two qubits are destroyed. Bob's qubit, b, now contains information about c; however, the information is somewhat randomized. More specifically, Bob's qubit b is in one of four states uniformly chosen at random and Bob cannot obtain any information about c from his qubit.
Alice provides her two measured classical bits, which indicate which of the four states Bob possesses. Bob applies a unitary transformation which depends on the classical bits he obtains from Alice, transforming his qubit into an identical re-creation of the qubit c.
, as:
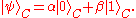
Our quantum teleportation scheme requires Alice and Bob to share a maximally entangled
state beforehand, for instance one of the four Bell state
s
,
,
,
.
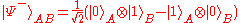Alice takes one of the particles in the pair, and Bob keeps the other one. The subscripts A and B in the entangled state refer to Alice's or Bob's particle. We will assume that Alice and Bob share the entangled state
So, Alice has two particles (C, the one she wants to teleport, and A, one of the entangled pair), and Bob has one particle, B. In the total system, the state of these three particles is given by
Alice will then make a partial measurement in the Bell basis on the two qubits in her possession. To make the result of her measurement clear, we will rewrite the two qubits of Alice in the Bell basis via the following general identities (these can be easily verified):
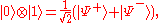
and
The three particle state shown above thus becomes the following four-term superposition:
Notice all we have done so far is a change of basis on Alice's part of the system. No operation has been performed and the three particles are still in the same state. The actual teleportation starts when Alice measures her two qubits in the Bell basis. Given the above expression, evidently the result of her (local) measurement is that the three-particle state would collapse to one of the following four states (with equal probability of obtaining each):
Alice's two particles are now entangled to each other, in one of the four Bell states. The entanglement originally shared between Alice's and Bob's is now broken. Bob's particle takes on one of the four superposition states shown above. Note how Bob's qubit is now in a state that resembles the state to be teleported. The four possible states for Bob's qubit
are unitary images of the state to be teleported.
The crucial step, the local measurement done by Alice on the Bell basis, is done. It is clear how to proceed further. Alice now has complete knowledge of the state of the three particles; the result of her Bell measurement tells her which of the four states the system is in. She simply has to send her results to Bob through a classical channel. Two classical bits can communicate which of the four results she obtained.
After Bob receives the message from Alice, he will know which of the four states his particle is in. Using this information, he performs a unitary operation on his particle to transform it to the desired state
:
to recover the state.
to his qubit.
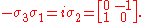
Teleportation is therefore achieved.
Experimentally, the projective measurement done by Alice may be achieved via a series of laser pulses directed at the two particles.
s. Direct calculation shows that this gate is given by
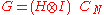
where H is the one qubit Walsh-Hadamard gate and
is the Controlled NOT gate
.
, that can be regarded as the state of a single subsystem of an entangled pair. The so-called entanglement swapping is a simple and illustrative example.
If Alice has a particle which is entangled with a particle owned by Bob, and Bob teleports it to Carol, then afterwards, Alice's particle is entangled with Carol's.
A more symmetric way to describe the situation is the following: Alice has one particle, Bob two, and Carol one. Alice's particle and Bob's first particle are entangled, and so are Bob's second and Carol's particle:
___
/ \
Alice-:-:-:-:-:-Bob1 -:- Bob2-:-:-:-:-:-Carol
\___/
Now, if Bob performs a projective measurement on his two particles in the Bell state basis and communicates the results to Carol, as per the teleportation scheme described above, the state of Bob's first particle can be teleported to Carol's. Although Alice and Carol never interacted with each other, their particles are now entangled.
dimensional state space. To teleport, Alice makes a partial measurement on the two particles in her possession in some entangled basis on the 
dimensional subsystem. This measurement has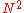 
equally probable outcomes, which are then communicated to Bob classically. Bob recovers the desired state by sending his particle through an appropriate unitary gate.
A successful teleportation process is a LOCC
quantum channel
Φ that satisfies
where Tr12 is the partial trace
operation with respect systems 1 and 2, and
denotes the composition of maps. This describes the channel in the Schrödinger picture.
Taking adjoint maps in the Heisenberg picture, the success condition becomes
for all observable O on Bob's system. The tensor factor in
is 
while that of 
is 
.
If the measurement registers the i-th outcome, the overall state collapses to
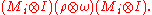
The tensor factor in
is 
while that of 
is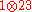 
. Bob then applies a corresponding local operation Ψi on system 3. On the combined system, this is described by
where Id is the identity map on the composite system
.
Therefore the channel Φ is defined by
Notice Φ satisfies the definition of LOCC
. As stated above, the teleportation is said to be successful if, for all observable O on Bob's system, the equality
holds. The left hand side of the equation is:
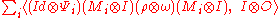
where Ψi* is the adjoint of Ψi in the Heisenberg picture. Assuming all objects are finite dimensional, this becomes
The success criterion for teleportation has the expression
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
(the basic unit of quantum information) can be transmitted exactly (in principle) from one location to another, without the qubit being transmitted through the intervening space. It is useful for quantum information processing
Quantum information science
Quantum information science is an area of study based on the idea that information science depends on quantum effects in physics. It includes theoretical issues in computational models as well as more experimental topics in quantum physics including what can and cannot be done with quantum...
, however it does not immediately transmit classical information, and therefore cannot be used for communication
Communication
Communication is the activity of conveying meaningful information. Communication requires a sender, a message, and an intended recipient, although the receiver need not be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast...
at superluminal (faster than light) speed. Quantum teleportation is unrelated to the common term teleportation - it does not transport the system itself, and does not concern rearranging particles to copy the form of an object.
The seminal paper first expounding the idea was published by Charles Bennett
Charles H. Bennett (computer scientist)
Charles H. Bennett is an IBM Fellow at IBM Research. Bennett's recent work at IBM has concentrated on a re-examination of the physical basis of information, applying quantum physics to the problems surrounding information exchange...
and coauthors in 1993. It was first confirmed experimentally in 1997 by a group in Innsbruck
Innsbruck
- Main sights :- Buildings :*Golden Roof*Kaiserliche Hofburg *Hofkirche with the cenotaph of Maximilian I, Holy Roman Emperor*Altes Landhaus...
and has subsequently been shown to work over distances of up to 16 kilometers.
Protocol
The prerequisites for quantum teleportation are a qubit that is to be teleported, a conventional communication channel capable of transmitting two classical bits (i.e., one of four states), and means of generating an entangledQuantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
EPR pair
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
of qubits, performing a Bell measurement on the EPR pair, and manipulating the quantum state of one of the pair. The protocol is then as follows:
1. An EPR pair is generated and distributed to two separate locations, A and B.
2. At location A, a Bell measurement of the EPR pair qubit and the qubit to be teleported (for example, quantum state
of a photon) is performed, yielding two classical bits of information. Both qubits are destroyed.3. Using the classical channel, the two bits are sent from A to B. (This is the only potentially time-consuming step, due to speed-of-light considerations.)
4. At location B, the EPR pair qubit is modified (if necessary), using the two bits to select the correct one of four possible quantum states. A qubit identical to that chosen for teleportation (for example, quantum state
of a photon) results.Experimental results
Work in 1998 verified the initial results, and in August 2004 increased the distance of teleportation to 600 meters using optical fiberOptical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
. The longest distance yet claimed to be achieved for quantum teleportation is 16 km (9.9 mi) in May 2010 by Chinese scientists over free-space with an average of 89% accuracy.
In April 2011, experimenters reported that they had demonstrated teleportation of wave packets of light up to a bandwidth of 10 MHz while preserving strongly nonclassical superposition states.
Motivation
Suppose AliceAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
has a qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
in some arbitrary quantum state
. (A qubit may be represented as a superpositionQuantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of states, labeled
and 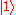.) Assume that this quantum state is not known to Alice and she would like to send this state to Bob. Ostensibly, Alice has the following options:- She can attempt to physically transport the qubit to Bob.
- She can broadcast this (quantum) information, and Bob can obtain the information via some suitable receiver.
- She can perhaps measure the unknown qubit in her possession. The results of this measurement would be communicated to Bob, who then prepares a qubit in his possession accordingly, to obtain the desired state. (This hypothetical process is called classical teleportation.)
Option 1 is highly undesirable because quantum states are fragile and any perturbation en route would corrupt the state.
Option 2 is forbidden by the no-broadcast theorem
No-broadcast theorem
The no-broadcast theorem is a result in quantum information theory. In the case of pure quantum states, it is a corollary of the no-cloning theorem: since quantum states cannot be copied in general, they cannot be broadcast...
.
Option 3 (classical teleportation) has also been formally shown to be impossible. (See the no teleportation theorem
No teleportation theorem
In quantum information theory, the no-teleportation theorem states that quantum information cannot be measured with complete accuracy.-Formulation:The term quantum information refers to information stored in the state of a quantum system...
.) This is another way to say that quantum information cannot be measured reliably.
Thus, Alice seems to face an impossible problem. A solution was discovered by Bennett, et al. The components of a maximally entangled two-qubit state are distributed to Alice and Bob. The protocol then involves Alice and Bob interacting locally with the qubit(s) in their possession and Alice sending two classical bits to Bob. In the end, the qubit in Bob's possession will be in the desired state.
A summary
Assume that Alice and Bob share an entangled qubit ab. That is, Alice has one half, a, and Bob has the other half, b. Let c denote the qubit Alice wishes to transmit to Bob.Alice applies a unitary operation on the qubits ac and measures the result to obtain two classical bits. In this process, the two qubits are destroyed. Bob's qubit, b, now contains information about c; however, the information is somewhat randomized. More specifically, Bob's qubit b is in one of four states uniformly chosen at random and Bob cannot obtain any information about c from his qubit.
Alice provides her two measured classical bits, which indicate which of the four states Bob possesses. Bob applies a unitary transformation which depends on the classical bits he obtains from Alice, transforming his qubit into an identical re-creation of the qubit c.
The result
Suppose Alice has a qubit that she wants to teleport to Bob. This qubit can be written generally, in bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
, as:
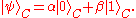
Our quantum teleportation scheme requires Alice and Bob to share a maximally entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
state beforehand, for instance one of the four Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s
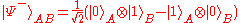,,,.Alice takes one of the particles in the pair, and Bob keeps the other one. The subscripts A and B in the entangled state refer to Alice's or Bob's particle. We will assume that Alice and Bob share the entangled state
So, Alice has two particles (C, the one she wants to teleport, and A, one of the entangled pair), and Bob has one particle, B. In the total system, the state of these three particles is given by
Alice will then make a partial measurement in the Bell basis on the two qubits in her possession. To make the result of her measurement clear, we will rewrite the two qubits of Alice in the Bell basis via the following general identities (these can be easily verified):
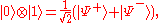
and
The three particle state shown above thus becomes the following four-term superposition:
Notice all we have done so far is a change of basis on Alice's part of the system. No operation has been performed and the three particles are still in the same state. The actual teleportation starts when Alice measures her two qubits in the Bell basis. Given the above expression, evidently the result of her (local) measurement is that the three-particle state would collapse to one of the following four states (with equal probability of obtaining each):
Alice's two particles are now entangled to each other, in one of the four Bell states. The entanglement originally shared between Alice's and Bob's is now broken. Bob's particle takes on one of the four superposition states shown above. Note how Bob's qubit is now in a state that resembles the state to be teleported. The four possible states for Bob's qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
are unitary images of the state to be teleported.
The crucial step, the local measurement done by Alice on the Bell basis, is done. It is clear how to proceed further. Alice now has complete knowledge of the state of the three particles; the result of her Bell measurement tells her which of the four states the system is in. She simply has to send her results to Bob through a classical channel. Two classical bits can communicate which of the four results she obtained.
After Bob receives the message from Alice, he will know which of the four states his particle is in. Using this information, he performs a unitary operation on his particle to transform it to the desired state
:- If Alice indicates her result is
, Bob knows his qubit is already in the desired state and does nothing. This amounts to the trivial unitary operation, the identity operator.
- If the message indicates
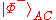, Bob would send his qubit through the unitary gate given by the Pauli matrix
to recover the state.
- If Alice's message corresponds to
, Bob applies the gate
to his qubit.
- Finally, for the remaining case, the appropriate gate is given by
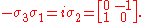
Teleportation is therefore achieved.
Experimentally, the projective measurement done by Alice may be achieved via a series of laser pulses directed at the two particles.
Remarks
- After this operation, Bob's qubit will take on the state
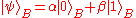, and Alice's qubit becomes (undefined) part of an entangled state. Teleportation does not result in the copying of qubits, and hence is consistent with the no cloning theoremNo cloning theoremThe no-cloning theorem is a result of quantum mechanics that forbids the creation of identical copies of an arbitrary unknown quantum state. It was stated by Wootters, Zurek, and Dieks in 1982, and has profound implications in quantum computing and related fields.The state of one system can be...
. - There is no transfer of matter or energy involved. Alice's particle has not been physically moved to Bob; only its state has been transferred. The term "teleportation", coined by Bennett, Brassard, Crépeau, Jozsa, Peres and Wootters, reflects the indistinguishability of quantum mechanical particles.
- For every qubit teleported, Alice needs to send Bob two classical bits of information. These two classical bits do not carry complete information about the qubit being teleported. If an eavesdropper intercepts the two bits, she may know exactly what Bob needs to do in order to recover the desired state. However, this information is useless if she cannot interact with the entangled particle in Bob's possession.
Alternative description
In the literature, one might find alternative, but completely equivalent, descriptions of the teleportation protocol given above. Namely, the unitary transformation that is the change of basis (from the standard product basis into the Bell basis) can also be implemented by quantum gateQuantum gate
In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s. Direct calculation shows that this gate is given by
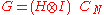
where H is the one qubit Walsh-Hadamard gate and
is the Controlled NOT gateControlled NOT gate
The Controlled NOT gate is a quantum gate that is an essential component in the construction of a quantum computer. It can be used to disentangle EPR states...
.
Entanglement swapping
Teleportation can be applied not just to pure states, but also mixed statesDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
, that can be regarded as the state of a single subsystem of an entangled pair. The so-called entanglement swapping is a simple and illustrative example.
If Alice has a particle which is entangled with a particle owned by Bob, and Bob teleports it to Carol, then afterwards, Alice's particle is entangled with Carol's.
A more symmetric way to describe the situation is the following: Alice has one particle, Bob two, and Carol one. Alice's particle and Bob's first particle are entangled, and so are Bob's second and Carol's particle:
___
/ \
Alice-:-:-:-:-:-Bob1 -:- Bob2-:-:-:-:-:-Carol
\___/
Now, if Bob performs a projective measurement on his two particles in the Bell state basis and communicates the results to Carol, as per the teleportation scheme described above, the state of Bob's first particle can be teleported to Carol's. Although Alice and Carol never interacted with each other, their particles are now entangled.
N-state particles
One can imagine how the teleportation scheme given above might be extended to N-state particles, i.e. particles whose states lie in the N dimensional Hilbert space. The combined system of the three particles now has a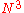 dimensional state space. To teleport, Alice makes a partial measurement on the two particles in her possession in some entangled basis on the 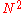dimensional subsystem. This measurement has 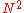equally probable outcomes, which are then communicated to Bob classically. Bob recovers the desired state by sending his particle through an appropriate unitary gate.General description
A general teleportation scheme can be described as follows. Three quantum systems are involved. System 1 is the (unknown) state ρ to be teleported by Alice. Systems 2 and 3 are in a maximally entangled state ω that are distributed to Alice and Bob, respectively. The total system is then in the stateA successful teleportation process is a LOCC
LOCC
LOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed...
quantum channel
Quantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
Φ that satisfies
where Tr12 is the partial trace
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
operation with respect systems 1 and 2, and
denotes the composition of maps. This describes the channel in the Schrödinger picture.Taking adjoint maps in the Heisenberg picture, the success condition becomes
for all observable O on Bob's system. The tensor factor in
is while that of is .Further details
The proposed channel Φ can be described more explicitly. To begin teleportation, Alice performs a local measurement on the two subsystems (1 and 2) in her possession. Assume the local measurement have effectsIf the measurement registers the i-th outcome, the overall state collapses to
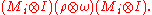
The tensor factor in
is while that of is 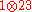. Bob then applies a corresponding local operation Ψi on system 3. On the combined system, this is described bywhere Id is the identity map on the composite system
.Therefore the channel Φ is defined by
Notice Φ satisfies the definition of LOCC
LOCC
LOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed...
. As stated above, the teleportation is said to be successful if, for all observable O on Bob's system, the equality
holds. The left hand side of the equation is:
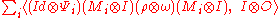
where Ψi* is the adjoint of Ψi in the Heisenberg picture. Assuming all objects are finite dimensional, this becomes
The success criterion for teleportation has the expression
See also
- Quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
- Introduction to quantum mechanicsIntroduction to quantum mechanicsQuantum mechanics is the body of scientific principles that explains the behavior of matter and its interactions with energy on the scale of atoms and atomic particles....
- Quantum nonlocalityQuantum nonlocalityQuantum nonlocality is the phenomenon by which measurements made at a microscopic level necessarily refute one or more notions that are regarded as intuitively true in classical mechanics...
- Quantum computers
- Quantum entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
- Heisenberg uncertainly principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
- Quantum energy teleportationQuantum energy teleportationQuantum energy teleportation is a hypothesis put forward first by Japanese physicist Masahiro Hotta of Tohoku University which proposes that it may be possible to teleport energy by exploiting quantum energy fluctuations of an entangled vacuum state of a quantum field...
- Introduction to quantum mechanics
External links
- signandsight.com:"Spooky action and beyond" - Interview with Prof. Dr. Anton ZeilingerAnton ZeilingerAnton Zeilinger is an Austrian quantum physicist. He is currently professor of physics at the University of Vienna, previously University of Innsbruck. He is also the director of the Vienna branch of the Institute for Quantum Optics and Quantum Information IQOQI at the Austrian Academy of Sciences...
about quantum teleportation. Date: 2006-02-16 - Quantum Teleportation at IBM
- Physicists Succeed In Transferring Information Between Matter And Light
- Quantum telecloning: Captain Kirk's clone and the eavesdropper
- Teleportation-based approaches to universal quantum computation
- Teleportation as a quantum computation
- Quantum teleportation with atoms: quantum process tomography
- Entangled State Teleportation
- Fidelity of quantum teleportation through noisy channels by
- TelePOVM— A generalized quantum teleportation scheme
- Entanglement Teleportation via Werner States
- Quantum Teleportation of a Polarization State
- The Time Travel Handbook: A Manual of Practical Teleportation & Time Travel
- letters to nature: Deterministic quantum teleportation with atoms
- Quantum teleportation with a complete Bell state measurement
- Welcome to the quantum Internet. Science News, Aug. 16 2008.
- Quantum experiments - interactive.
- “A (mostly serious) introduction to quantum teleportation for non-physicists”