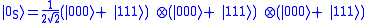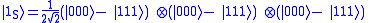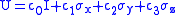Quantum error correction
Encyclopedia
Quantum error correction is used in quantum computing
to protect quantum information
from errors due to decoherence and other quantum noise
. Quantum error correction is essential if one is to achieve fault-tolerant quantum computation that can deal not only with noise on stored quantum information, but also with faulty quantum gates, faulty quantum preparation, and faulty measurements.
Classical error correction employs redundancy
. The simplest way is to store the information multiple times, and—if these copies are later found to disagree—just take a majority vote; e.g.
Suppose we copy a bit three times. Suppose further that a noisy error corrupts the three-bit state so that one bit is equal to zero but the other two are equal to one. We also assume that noisy errors are independent and occur with some probability p. It is most likely that the error is a single-bit error and the transmitted message is three ones. It is possible that a double-bit error occurs and the transmitted message is equal to three zeros, but this outcome is less likely than the above outcome.
Copying quantum information is not possible due to the no-cloning theorem. This theorem seems to present an obstacle to formulating a theory of quantum error correction. But it is possible to spread the information of one qubit
onto a highly-entangled state of several (physical) qubits. Peter Shor first discovered this method of formulating a quantum error correcting code by storing the information of one qubit onto a highly-entangled state of nine qubits. A quantum error correcting code protects quantum information against errors of a limited form.
Classical error correcting codes use a syndrome measurement to diagnose which error corrupts an encoded state. We then reverse an error by applying a corrective operation based on the syndrome. Quantum error correction also employs syndrome measurements. We perform a multi-qubit measurement that does not disturb the quantum information in the encoded state but retrieves information about the error. A syndrome measurement can determine whether a qubit has been corrupted, and if so, which one. What is more, the outcome of this operation (the syndrome) tells us not only which physical qubit was affected, but also, in which of several possible ways it was affected. The latter is counter-intuitive at first sight: Since noise is arbitrary, how can the effect of noise be one of only few distinct possibilities? In most codes, the effect is either a bit flip, or a sign (of the phase
) flip, or both (corresponding to the Pauli matrices
X, Z, and Y). The reason is that the measurement of the syndrome has the projective
effect of a quantum measurement. So even if the error due to the noise was arbitrary, it can be expressed as a superposition
of basis
operations—the error basis (which is here given by the Pauli matrices and the identity
).
The syndrome measurement "forces" the qubit to "decide" for a certain specific "Pauli error" to "have happened", and the syndrome tells us which, so that we can let the same Pauli operator act again on the corrupted qubit to revert the effect of the error.
The syndrome measurement tells us as much as possible about the error that has happened, but nothing at all about the value that is stored in the logical qubit—as otherwise the measurement would destroy any quantum superposition
of this logical qubit with other qubits in the quantum computer
.
Let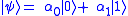
be an arbitrary qubit. The first step of the three qubit bit flip code is to entangle the qubit with two other qubits using two CNOT gates
with input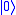
. The result will be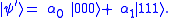 
This is just a tensor product of three qubits, and different from cloning a state.
Now these qubits will be sent through a channel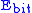
where we assume that at most one bit flip may occur. For example, in the case where the first qubit were be flipped, the result would be 
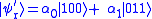. To diagnose bit flips in any of the three possible qubits, syndrome diagnosis is needed, which includes four projection operators:
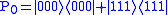
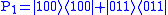
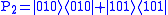
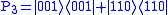
It can be obtained:
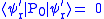
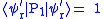
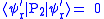
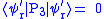
So it will be known that the error syndrome corresponding to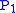
.
This three qubits bit flip code can correct one error if at most one bit-flip-error occurred in the channel. It is similar to the three bits repetition code in a classical computer.
and 
can become inverted. For instance, a qubit in the state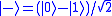 
may have its sign flip to 
The original state of the qubit
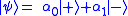
will be changed into the state
In the Hadamard basis, bit flips become sign flips and sign flips become bit flips. Let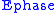
be a quantum channel that can cause at most one phase flip. Then the bit flip code from above can recover 
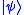by transforming into the Hadamard basis before and after transmission through 
.
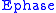Let
be a quantum channel that can arbitrarily corrupt a single qubit. The 1st, 4th and 7th qubits are for the sign flip code, while the three group of qubits (1,2,3), (4,5,6), and (7,8,9) are designed for the bit flip code. With the Shor code, a qubit state 
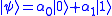will be transformed into the product of 9 qubits 
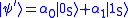, where
If a bit flip error happens to a qubit, the syndrome analysis will be performed on each set of states (1,2,3), (4,5,6), and (7,8,9), then correct the error.
If the three bit flip group (1,2,3), (4,5,6), and (7,8,9) are considered as three inputs, then the Shor code circuit can be reduced as a sign flip code. This means that the Shor code can also repair sign flip error for a single qubit.
The Shor code also can correct for any arbitrary errors (both bit flip and sign flip) to a single qubit. If an error is modeled by a unitary transform U, which will act on a qubit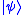
, then 
can be described in the form
where
,
,
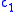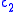, and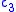 
are complex constants, I is the identity, and the Pauli matrices
are given by
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
to protect quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
from errors due to decoherence and other quantum noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
. Quantum error correction is essential if one is to achieve fault-tolerant quantum computation that can deal not only with noise on stored quantum information, but also with faulty quantum gates, faulty quantum preparation, and faulty measurements.
Classical error correction employs redundancy
Redundancy (information theory)
Redundancy in information theory is the number of bits used to transmit a message minus the number of bits of actual information in the message. Informally, it is the amount of wasted "space" used to transmit certain data...
. The simplest way is to store the information multiple times, and—if these copies are later found to disagree—just take a majority vote; e.g.
Suppose we copy a bit three times. Suppose further that a noisy error corrupts the three-bit state so that one bit is equal to zero but the other two are equal to one. We also assume that noisy errors are independent and occur with some probability p. It is most likely that the error is a single-bit error and the transmitted message is three ones. It is possible that a double-bit error occurs and the transmitted message is equal to three zeros, but this outcome is less likely than the above outcome.
Copying quantum information is not possible due to the no-cloning theorem. This theorem seems to present an obstacle to formulating a theory of quantum error correction. But it is possible to spread the information of one qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
onto a highly-entangled state of several (physical) qubits. Peter Shor first discovered this method of formulating a quantum error correcting code by storing the information of one qubit onto a highly-entangled state of nine qubits. A quantum error correcting code protects quantum information against errors of a limited form.
Classical error correcting codes use a syndrome measurement to diagnose which error corrupts an encoded state. We then reverse an error by applying a corrective operation based on the syndrome. Quantum error correction also employs syndrome measurements. We perform a multi-qubit measurement that does not disturb the quantum information in the encoded state but retrieves information about the error. A syndrome measurement can determine whether a qubit has been corrupted, and if so, which one. What is more, the outcome of this operation (the syndrome) tells us not only which physical qubit was affected, but also, in which of several possible ways it was affected. The latter is counter-intuitive at first sight: Since noise is arbitrary, how can the effect of noise be one of only few distinct possibilities? In most codes, the effect is either a bit flip, or a sign (of the phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
) flip, or both (corresponding to the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
X, Z, and Y). The reason is that the measurement of the syndrome has the projective
Projective
-About :Projective provides project management services for financial institutions. According to the firm's website, Projective currently has three branches . The headquarter is located in Kontich, Belgium...
effect of a quantum measurement. So even if the error due to the noise was arbitrary, it can be expressed as a superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
operations—the error basis (which is here given by the Pauli matrices and the identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
).
The syndrome measurement "forces" the qubit to "decide" for a certain specific "Pauli error" to "have happened", and the syndrome tells us which, so that we can let the same Pauli operator act again on the corrupted qubit to revert the effect of the error.
The syndrome measurement tells us as much as possible about the error that has happened, but nothing at all about the value that is stored in the logical qubit—as otherwise the measurement would destroy any quantum superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of this logical qubit with other qubits in the quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
.
The bit flip code
The repetition code works in a classical channel, because classical bits are easy to measure and to repeat. However, in a quantum channel, it is no longer possible, due to the no-cloning theorem, which forbids the creation of identical copies of an arbitrary unknown quantum state. So a single qubit can not be repeated three times as in the previous example, as any measurement of the qubit will change its wave function. Nevertheless, in a quantum computer, there is another method, which is called the three qubits bit flip code. It uses entanglement and syndrome measurements, and can perform the similar results to the repetition code.Let
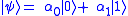be an arbitrary qubit. The first step of the three qubit bit flip code is to entangle the qubit with two other qubits using two CNOT gatesControlled NOT gate
The Controlled NOT gate is a quantum gate that is an essential component in the construction of a quantum computer. It can be used to disentangle EPR states...
with input
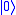. The result will be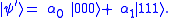 This is just a tensor product of three qubits, and different from cloning a state.
Now these qubits will be sent through a channel
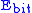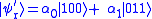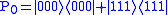
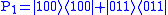
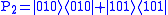
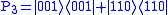
where we assume that at most one bit flip may occur. For example, in the case where the first qubit were be flipped, the result would be . To diagnose bit flips in any of the three possible qubits, syndrome diagnosis is needed, which includes four projection operators:It can be obtained:
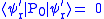
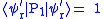
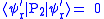
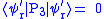
So it will be known that the error syndrome corresponding to
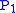.This three qubits bit flip code can correct one error if at most one bit-flip-error occurred in the channel. It is similar to the three bits repetition code in a classical computer.
The sign flip code
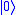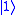Flipped bits are the only kind of error in classical computer, but there is another possibility of an error with quantum computers, the sign flip. Through the transmission in a channel the relative sign between and can become inverted. For instance, a qubit in the state 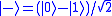may have its sign flip to The original state of the qubit
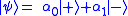
will be changed into the state
In the Hadamard basis, bit flips become sign flips and sign flips become bit flips. Let
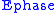be a quantum channel that can cause at most one phase flip. Then the bit flip code from above can recover 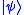by transforming into the Hadamard basis before and after transmission through 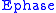.The Shor code
The error channel may induce either a bit flip, a sign flip, or both. It is possible to correct for both types of errors using one code, and the Shor code does just that. In fact, the Shor code corrects arbitrary single-qubit errors.Let
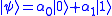be a quantum channel that can arbitrarily corrupt a single qubit. The 1st, 4th and 7th qubits are for the sign flip code, while the three group of qubits (1,2,3), (4,5,6), and (7,8,9) are designed for the bit flip code. With the Shor code, a qubit state will be transformed into the product of 9 qubits 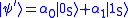, where
If a bit flip error happens to a qubit, the syndrome analysis will be performed on each set of states (1,2,3), (4,5,6), and (7,8,9), then correct the error.
If the three bit flip group (1,2,3), (4,5,6), and (7,8,9) are considered as three inputs, then the Shor code circuit can be reduced as a sign flip code. This means that the Shor code can also repair sign flip error for a single qubit.
The Shor code also can correct for any arbitrary errors (both bit flip and sign flip) to a single qubit. If an error is modeled by a unitary transform U, which will act on a qubit
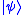, then can be described in the form
where
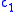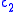,,, and 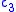are complex constants, I is the identity, and the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
are given by
-
-
-
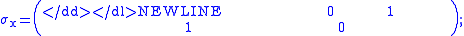
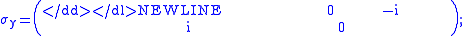
If U is equal to I, then no error occurs. If
, a bit flip error occurs. If 
, a sign flip error occurs. If 
then both a bit flip error and a sign flip error occur. Due to linearity, it follows that the Shor code can correct arbitrary 1-qubit errors.
General codes
In general, a quantum code for a quantum channelQuantum channelIn quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
is a subspace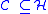 
, where 
is the state Hilbert space, such that there exists another quantum channel 
with
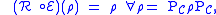
where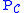
is the orthogonal projection onto 
. Here 
is known as the correction operation.
Models
Over time, researchers have come up with several codes:
- Peter ShorPeter ShorPeter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
's 9-qubit-code, a.k.a. the Shor code, encodes 1 logical qubit in 9 physical qubits and can correct for arbitrary errors in a single qubit. - Andrew SteaneAndrew SteaneAndrew Martin Steane is Professor of physics at the University of Oxford. He is also a fellow of Exeter College, Oxford.He was a student at St Edmund Hall, Oxford where he obtained his MA and DPhil....
found a code which does the same with 7 instead of 9 qubits, see Steane codeSteane codeThe Steane code is a tool in quantum error correction introduced by Andrew Steane in 1996. It is a perfect CSS code , using the classical binary self-dual [7,4,3] Hamming code to correct for qubit flip errors and the dual of the Hamming code, the [7,3,3] code, to correct for phase flip errors...
. - Raymond LaflammeRaymond LaflammeRaymond Laflamme is a physicist and the co-founder and current director of the Institute for Quantum Computing. He is also an associate faculty member at Perimeter Institute for Theoretical Physics. He was a doctoral student of Stephen Hawking at the University of Cambridge. He is responsible for...
found a class of 5-qubit codes which do the same, which also have the property of being fault-tolerant. - A generalisation of this concept are the CSS codeCSS codeIn quantum error correction, CSS codes, named after their inventors, A. R. Calderbank, Peter Shor and Andrew Steane, are a special type of Stabilizer codes constructed from classical codes with some special properties.- Construction :...
s, named for their inventors: A. R. Calderbank, Peter ShorPeter ShorPeter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
and Andrew SteaneAndrew SteaneAndrew Martin Steane is Professor of physics at the University of Oxford. He is also a fellow of Exeter College, Oxford.He was a student at St Edmund Hall, Oxford where he obtained his MA and DPhil....
. According to the quantum Hamming bound, encoding a single logical qubit and providing for arbitrary error correction in a single qubit requires a minimum of 5 physical qubits. - A more general class of codes (encompassing the former) are the stabilizer codeStabilizer codeThe theory of quantum error correction plays a prominent role in the practical realization and engineering ofquantum computing and quantum communication devices. The first quantumerror-correcting codes are strikingly similar to classical block codes in their...
s discovered by Daniel GottesmanDaniel GottesmanDaniel Gottesman is a physicist, known for his work regarding quantum error correction, in particular the invention of the stabilizer formalism for quantum error-correcting codes, and the Gottesman–Knill theorem...
(http://arxiv.org/abs/quant-ph/9604038), and by A. R. Calderbank, Eric Rains, Peter ShorPeter ShorPeter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
, and N. J. A. Sloane (http://arxiv.org/abs/quant-ph/9605005, http://arxiv.org/abs/quant-ph/9608006); these are also called additive codes. - A newer idea is Alexei KitaevAlexei KitaevAlexei Kitaev is a professor of physics and computer science at the California Institute of Technology. He is best known for introducing the quantum phase estimation algorithm and the concept of the topological quantum computer while working at the Landau Institute for Theoretical Physics. For...
's topological quantum codeToric codeThe Toric Code is a topological quantum error correcting code, and an example of a stabilizer code, defined on a two dimensional spin lattice It is the simplest and most well studied of the quantum double models...
s and the more general idea of a topological quantum computerTopological quantum computerA topological quantum computer is a theoretical quantum computer that employs two-dimensional quasiparticles called anyons, whose world lines cross over one another to form braids in a three-dimensional spacetime . These braids form the logic gates that make up the computer...
. - Todd Brun, Igor Devetak, and Min-Hsiu Hsieh also constructed the entanglement-assisted stabilizer formalismEntanglement-assisted stabilizer formalismIn the theory of quantum communication, the entanglement-assisted stabilizer formalism is a method for protecting quantum information with the help of entanglement shared between a sender and receiver before they transmit quantum data over a quantum communication channel...
as an extension of the standard stabilizer formalism that incorporates quantum entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
shared between a sender and a receiver.
That these codes allow indeed for quantum computations of arbitrary length is the content of the threshold theorem, found by Michael Ben-Or and Dorit AharonovDorit AharonovDorit Aharonov is an Israeli computer scientist specializing in quantum computing.Aharonov graduated from Hebrew University of Jerusalem with a BSc in Mathematics and Physics in 1994. She then graduated from Weizmann Institute of Science with an MSc in Physics...
, which asserts that you can correct for all errors if you concatenate quantum codes such as the CSS codes—i.e. re-encode each logical qubit by the same code again, and so on, on logarithmically many levels—provided the error rate of individual quantum gateQuantum gateIn quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s is below a certain threshold; as otherwise, the attempts to measure the syndrome and correct the errors would introduce more new errors than they correct for.
As of late 2004, estimates for this threshold indicate that it could be as high as 1-3% http://www.arxiv.org/abs/quant-ph/0410199, provided that there are sufficiently many qubitQubitIn quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s available.
Experimental Realization
There have been several experimental realizations of CSS-based codes. The first demonstration with was with NMR qubits. Subsequently demonstrations have been made with linear optics, trapped ions, and superconducting (transmon) qubits.
Other error correcting codes have also been implemented, such as one aimed at correcting for photon loss, the dominant error source in photonic qubit schemes.
External links
- Peter Shor
-
-