Quadrupole ion trap
Encyclopedia
Ion trap
An ion trap is a combination of electric or magnetic fields that captures ions in a region of a vacuum system or tube. Ion traps have a number of scientific uses such as mass spectrometery and trapping ions while the ion's quantum state is manipulated...
that uses constant DC
Direct current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
and radio frequency
Radio frequency
Radio frequency is a rate of oscillation in the range of about 3 kHz to 300 GHz, which corresponds to the frequency of radio waves, and the alternating currents which carry radio signals...
(RF) oscillating AC
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
s to trap ions. It is commonly used as a component of a mass spectrometer. The invention of the 3D quadrupole ion trap itself is attributed to Wolfgang Paul
Wolfgang Paul
Wolfgang Paul was a German physicist, who co-developed the non-magnetic quadrupole mass filter which laid the foundation for what we now call an ion trap...
who shared the Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
in 1989 for this work.
Theory
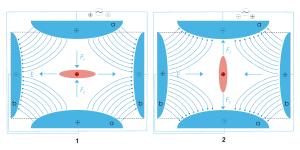
The 3D trap itself generally consists of two hyperbolicHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
metal electrodes with their foci facing each other and a hyperbolic ring electrode halfway between the other two electrodes. The ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s are trapped in the space between these three electrodes by AC (oscillating, non-static) and DC (non-oscillating, static) electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
s. The AC radio frequency voltage oscillates between the two hyperbolic
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
metal end cap electrodes if ion excitation is desired; the driving AC voltage is applied to the ring electrode. The ions are first pulled up and down axially while being pushed in radially. The ions are then pulled out radially and pushed in axially (from the top and bottom). In this way the ions move in a complex motion that generally involves the cloud of ions being long and narrow and then short and wide, back and forth, oscillating between the two states. Since the mid-1980s most 3D traps (Paul traps) have used ~1 mtorr of helium. The use of damping gas and the mass-selective instability mode developed by Stafford et al. led to the first commercial 3D ion traps.
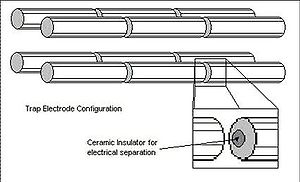
Rectilinear polygon
A rectilinear polygon is a polygon all of whose edges meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons....
configuration has also been used. The advantage of the linear design is in its simplicity, but this leaves a particular constraint on its modeling. To understand how this originates, it is helpful to visualize the linear form. The Paul trap is designed to create a saddle-shaped field to trap a charged ion, but with a quadrupole, this saddle-shaped electric field cannot be rotated about an ion in the centre. It can only 'flap' the field up and down. For this reason, the motions of a single ion in the trap are described by the Mathieu Equations
Mathieu function
In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...
. These equations can only be solved numerically, or equivalently by computer simulations.
The intuitive explanation and lowest order approximation is the same as strong focusing
Strong focusing
In accelerator physics strong focusing or alternating-gradient focusing is the principle that the net effect on a particle beam of charged particles passing through alternating field gradients is to make the beam converge...
in accelerator physics
Accelerator physics
Accelerator physics deals with the problems of building and operating particle accelerators.The experiments conducted with particle accelerators are not regarded as part of accelerator physics. These belong to particle physics, nuclear physics, condensed matter physics, materials physics, etc...
. Since the field affects the acceleration, the position lags behind (to lowest order by half a period). So the particles are at defocused positions when the field is focusing and vice versa. Being farther from center, they experience a stronger field when the field is focusing than when it is defocusing.
Equations of motion
Ions in a quadrupole field experience restoring forces that drive them back toward the center of the trap. The motion of the ions in the field is described by solutions to the Mathieu equationMathieu function
In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...
. When written for ion motion in a trap, the equation is
where
represents the x, y and z coordinated, 
is a dimensionless parameter given by 
, and 
and 
are dimensionless trapping parameters. The parameter 
is the radial frequency of the potential applied to the ring electrode. By substituting the expression for 
into Equation 1, it can be shown that
Substituting Equation 2 into the Matthieu Equation 1 yields
.Reorganizing terms shows us that
.By Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, the above equation represents the force on the ion. This equation can be exactly solved using Floquet theorem or the standard techniques of multiple scale analysis . The particle dynamics and time averaged density of charged particles in a Paul trap can also be obtained by the concept of ponderomotive force.
The forces in each dimension are not coupled, thus the force acting on an ion in, for example, the x dimension is
Here,
is the quadrupolar potential, given by
where
is the applied electric potential and 
, 
, and 
are weighting factors, and 
is a size parameter constant. In order to satisfy the Laplace ConditionLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
,
, it can be shown that
.For an ion trap,
and 
and for a quadrupole mass filter, 
and 
.Transforming Equation 5 into a cylindrical coordinate system
Cylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
with
, 
, and 
and applying the pythagorean trigonometric identityPythagorean trigonometric identity
The Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
gives
The applied electric potential is a combination of RF and DC given by
where
and 
is the applied frequency in hertzHertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
.
Substituting Equation 7 into Equation 5 with
gives
Substituting Equation 8 into Equation 4 leads to
Comparing terms on the right hand side of Equation 1 and Equation 9 leads to
and
Further
,
and
The trapping of ions can be understood in terms of stability regions in
and 
space.Linear ion trap
