
Q (number format)
Encyclopedia
Q is a fixed point
number format where the number of fractional
bit
s (and optionally the number of integer
bits) is specified. For example, a Q15 number has 15 fractional bits; a Q1.14 number has 1 integer bit and 14 fractional bits. Q format is often used in hardware that does not have a floating-point unit and in applications that require constant resolution
.
to perform rational number
calculations. The number of integer bits, fractional bits and the underlying word size are to be chosen by the programmer on an application-specific basis — the programmer's choices of the foregoing will depend on the range and resolution needed for the numbers. The machine itself remains oblivious to the notional fixed point representation being employed — it merely performs integer arithmetic the way it knows how. Ensuring that the computational results are valid in the Q format representation is the responsibility of the programmer.
The Q notation is written as Qm.n, where:
Note that the most significant bit is always designated as the sign bit (the number is stored as a two's complement
number) in order to allow standard arithmetic-logic hardware to manipulate Q numbers. Representing a signed fixed-point data type in Q format therefore always requires m+n+1 bits to account for the sign bit. Hence the smallest machine word size required to accommodate a Qm.n number is m+n+1, with the Q number left justified in the machine word.
For a given Qm.n format, using an m+n+1 bit signed integer container with n fractional bits:
For example, a Q14.1 format number:
Unlike floating point
numbers, the resolution of Q numbers will remain constant over the entire range.
Consider the following example:
The Q8 denominator equals 28 = 256
1.5 equals 384/256
384 is stored, 256 is inferred because it is a Q8 number.
If the Q number's base is to be maintained (n remains constant) the Q number math operations must keep the denominator constant.
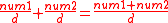
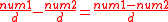
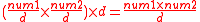
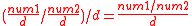
Because the denominator is a power of two the multiplication can be implemented as an arithmetic shift
to the left and the division as an arithmetic shift to the right; on many processors shifts are faster than multiplication and division.
To maintain accuracy the intermediate multiplication and division results must be double precision and care must be taken in rounding
the intermediate result before converting back to the desired Q number.
Using C
the operations are (note that here, Q refers to the fractional part's number of bits) :
#define K (1 << (Q-1))
signed int a, b, result;
signed long int temp;
temp = (long int) a * (long int) b; // result type is operand's type
// Rounding; mid values are rounded up
temp += K;
// Correct by dividing by base
result= temp >> Q;
signed long int temp;
// pre-multiply by the base (Upscale to Q16 so that the result will be in Q8 format)
temp = (long int)a << Q;
// So the result will be rounded ; mid values are rounded up.
temp = temp+b/2;
result = temp/b;
Fixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
number format where the number of fractional
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s (and optionally the number of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
bits) is specified. For example, a Q15 number has 15 fractional bits; a Q1.14 number has 1 integer bit and 14 fractional bits. Q format is often used in hardware that does not have a floating-point unit and in applications that require constant resolution
Fixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
.
Characteristics
Q format numbers are (notionally) fixed point numbers (but not actually a number itself); that is, they are stored and operated upon as regular binary numbers (i.e. signed integers), thus allowing standard integer hardware/ALUArithmetic logic unit
In computing, an arithmetic logic unit is a digital circuit that performs arithmetic and logical operations.The ALU is a fundamental building block of the central processing unit of a computer, and even the simplest microprocessors contain one for purposes such as maintaining timers...
to perform rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
calculations. The number of integer bits, fractional bits and the underlying word size are to be chosen by the programmer on an application-specific basis — the programmer's choices of the foregoing will depend on the range and resolution needed for the numbers. The machine itself remains oblivious to the notional fixed point representation being employed — it merely performs integer arithmetic the way it knows how. Ensuring that the computational results are valid in the Q format representation is the responsibility of the programmer.
The Q notation is written as Qm.n, where:
- Q designates that the number is in the Q format notation — the Texas InstrumentsTexas InstrumentsTexas Instruments Inc. , widely known as TI, is an American company based in Dallas, Texas, United States, which develops and commercializes semiconductor and computer technology...
representation for signed fixed-point numbers (the "Q" being reminiscent of the standard symbol for the set of rational numbersRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
). - m is the number of bits set aside to designate the two's complement integer portion of the number, exclusive of the sign bit (therefore if m is not specified it is taken as zero).
- n is the number of bits used to designate the fractional portion of the number, i.e. the number of bits to the right of the binary point. (If n = 0, the Q numbers are integers — the degenerate case).
Note that the most significant bit is always designated as the sign bit (the number is stored as a two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
number) in order to allow standard arithmetic-logic hardware to manipulate Q numbers. Representing a signed fixed-point data type in Q format therefore always requires m+n+1 bits to account for the sign bit. Hence the smallest machine word size required to accommodate a Qm.n number is m+n+1, with the Q number left justified in the machine word.
For a given Qm.n format, using an m+n+1 bit signed integer container with n fractional bits:
- its range is [-2m, 2m - 2-n]
- its resolution is 2-n
For example, a Q14.1 format number:
- requires 14+1+1 = 16 bits
- its range is [-214, 214 - 2−1] = [-16384.0, +16383.5] = [0x8000, 0x8001 … 0xFFFF, 0x0000, 0x0001 … 0x7FFE, 0x7FFF]
- its resolution is 2−1 = 0.5
Unlike floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
numbers, the resolution of Q numbers will remain constant over the entire range.
Float to Q
To convert a number from floating point to Qm.n format:- Multiply the floating point number by 2n
- Round to the nearest integer
Q to float
To convert a number from Qm.n format to floating point:- Convert the number to floating point as if it were an integer
- Multiply by 2−n
Math operations
Q numbers are a ratio of two integers: the numerator is kept in storage, the denominator is equal to 2n.Consider the following example:
The Q8 denominator equals 28 = 256
1.5 equals 384/256
384 is stored, 256 is inferred because it is a Q8 number.
If the Q number's base is to be maintained (n remains constant) the Q number math operations must keep the denominator constant.
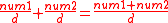
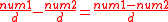
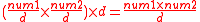
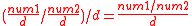
Because the denominator is a power of two the multiplication can be implemented as an arithmetic shift
Arithmetic shift
In computer programming, an arithmetic shift is a shift operator, sometimes known as a signed shift . For binary numbers it is a bitwise operation that shifts all of the bits of its operand; every bit in the operand is simply moved a given number of bit positions, and the vacant bit-positions are...
to the left and the division as an arithmetic shift to the right; on many processors shifts are faster than multiplication and division.
To maintain accuracy the intermediate multiplication and division results must be double precision and care must be taken in rounding
Rounding
Rounding a numerical value means replacing it by another value that is approximately equal but has a shorter, simpler, or more explicit representation; for example, replacing $23.4476 with $23.45, or the fraction 312/937 with 1/3, or the expression √2 with 1.414.Rounding is often done on purpose to...
the intermediate result before converting back to the desired Q number.
Using C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
the operations are (note that here, Q refers to the fractional part's number of bits) :
Multiplication
// precomputed value:#define K (1 << (Q-1))
signed int a, b, result;
signed long int temp;
temp = (long int) a * (long int) b; // result type is operand's type
// Rounding; mid values are rounded up
temp += K;
// Correct by dividing by base
result= temp >> Q;
Division
signed int a,b,result;signed long int temp;
// pre-multiply by the base (Upscale to Q16 so that the result will be in Q8 format)
temp = (long int)a << Q;
// So the result will be rounded ; mid values are rounded up.
temp = temp+b/2;
result = temp/b;
See also
- Binary scalingBinary scalingBinary scaling is a computer programming technique used mainly by embedded C, DSP and assembler programmers to perform a pseudo floating point using integer arithmetic....
- Fixed-point arithmeticFixed-point arithmeticIn computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
- Floating pointFloating pointIn computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
External links
- Fixed Point Representation And Fractional Math (Note: the accuracy of the article is in dispute; see discussion.)

