Binary scaling
Encyclopedia
Binary scaling is a computer programming
technique used mainly by embedded C
, DSP
and assembler
programmers to perform a pseudo floating point
using integer
arithmetic.
It is both faster and more accurate than directly using floating point instructions, however care must be taken not to cause an arithmetic overflow
.
A position for the virtual 'binary point' is taken, and then subsequent arithmetic operations
determine the resultants 'binary point'.
Binary points obey the mathematical laws of exponentiation
.
To give an example, a common way to use integer arithmetic
to simulate floating point is to multiply the coefficients by 65536.
This will place the binary point at B16.
For instance to represent 1.2 and 5.6 floating point real numbers as B16 one multiplies them by 216 giving
78643 and 367001
Multiplying these together gives
28862059643
To convert it back to B16, divide it by 216.
This gives 440400B16, which when converted back to a floating point number (by dividing again by 216, but holding the result as floating point) gives 6.71999.
The correct floating point result is 6.72.
The scaling range here is for any number between 65535.9999 and -65536.0 with 16 bits to hold fractional quantities (of course assuming the use of a 64 bit result register). Note that some computer architectures may restrict arithmetic to 32 bit results. In this case extreme care must be taken not to overflow the 32 bit register. For other number ranges the binary scale can be adjusted for optimum accuracy.
Consider the Binary Point in a signed 32 bit word thus:
0 1 2 3 4 5 6 7 8 9
S X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X
where S is the sign bit and X are the other bits.
Placing the binary point at
When using different B scalings the complete B scaling formula must be used.
Consider a 32 bit word size, and two variables, one with a B scaling of 2 and the other with a scaling of 4.
1.4 @ B2 is 1.4 * (2wordsize-2-1)
Note that here the 1.4 values is very well represented with 30 fraction bits! A 32 bit real number
has 23 bits to store the fraction in. This is why B scaling is always more accurate than floating point of the same word size.
This is especially useful in integrator
s or repeated summing of small quantities where rounding error can be a subtle but very dangerous problem, when using floating point.
Now a larger number 15.2 at B4.
15.2 @ B4 is 15.2 * (2 ^ (wordsize-4-1))
Again the number of bits to store the fraction is 28 bits.
Multiplying these 32 bit numbers give the 64 bit result 0x1547AE14A51EB852
This result is in B7 in a 64 bit word. Shifting it down by 32 bits gives the result in B7 in 32 bits.
0x1547AE14
To convert back to floating point, divide this by (2^(wordsize-7-1)) 21.2800000099
Binary angles
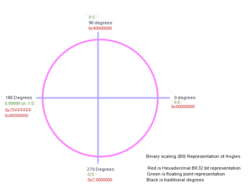Binary angles are mapped using B0, with 0 as 0 degrees, 0.5 as 90 (or 
), −1.0 or 0.9999999 as 180 (or π) and −0.5 as 270 (or 
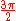). When these binary angles are added using normal two's complement
mathematics the rotation of the angles is correct, even when crossing the sign boundary (this of course does away with checks for angle ≥ 360 when handling normal degrees).
The terms Binary Angular Measurement System (BAMS) and 'brads' (binary radians) refer to implementations of binary angles. They find use in robotics, navigation, computer games, digital sensors and weapons system's digital communications Binary angles may be thought of as the fractional part of an angle when expressed in units of turn
.
No matter what bit-pattern is stored in a binary angle, when it is multiplied by 360 (or 2π) using standard signed fixed-point arithmetic
, the result is always a valid angle in the range of -180 degrees (-π radians) to +180 degrees (+π radians).
In some cases, it is convenient to use unsigned multiplication (rather than signed multiplication) on a binary angle, which gives the correct angle in the range of 0 to +360 degrees (+2π radians).
Compared to storing angles in a binary angle format, storing angles in any other format inevitably results in some bit patterns giving "angles" outside that range, requiring extra steps to range-reduce the value to the desired range, or results in some bit patterns that are not valid angles at all (NaN
), or both.
Application of binary scaling techniques
Binary scaling techniques were used in the 1970s and 80s for real time computing that was mathematically intensive, such as flight simulation. The code was often commented with the binary scalings of the intermediate results of equations.
Binary scaling is still used in many DSP
applications and custom made microprocessors are usually based on binary scaling techniques.
Binary scaling is currently used in the DCT
used to compress JPEG
images in utilities such as the GIMP
.
Although floating point has taken over to a large degree, where speed and extra accuracy are required, binary scaling works on simpler hardware and is more accurate when the range of values is known in advance.
Computer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
technique used mainly by embedded C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, DSP
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
and assembler
Assembly language
An assembly language is a low-level programming language for computers, microprocessors, microcontrollers, and other programmable devices. It implements a symbolic representation of the machine codes and other constants needed to program a given CPU architecture...
programmers to perform a pseudo floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
using integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
arithmetic.
It is both faster and more accurate than directly using floating point instructions, however care must be taken not to cause an arithmetic overflow
Arithmetic overflow
The term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
.
A position for the virtual 'binary point' is taken, and then subsequent arithmetic operations
determine the resultants 'binary point'.
Binary points obey the mathematical laws of exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
.
To give an example, a common way to use integer arithmetic
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
to simulate floating point is to multiply the coefficients by 65536.
This will place the binary point at B16.
For instance to represent 1.2 and 5.6 floating point real numbers as B16 one multiplies them by 216 giving
78643 and 367001
Multiplying these together gives
28862059643
To convert it back to B16, divide it by 216.
This gives 440400B16, which when converted back to a floating point number (by dividing again by 216, but holding the result as floating point) gives 6.71999.
The correct floating point result is 6.72.
The scaling range here is for any number between 65535.9999 and -65536.0 with 16 bits to hold fractional quantities (of course assuming the use of a 64 bit result register). Note that some computer architectures may restrict arithmetic to 32 bit results. In this case extreme care must be taken not to overflow the 32 bit register. For other number ranges the binary scale can be adjusted for optimum accuracy.
Re-scaling after multiplication
The example above for a B16 multiplication is a simplified example. Re-scaling depends on both the B scale value and the word size. B16 is often used in 32 bit systems because it works simply by multiplying and dividing by 65536 (or shifting 16 bits).Consider the Binary Point in a signed 32 bit word thus:
0 1 2 3 4 5 6 7 8 9
S X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X
where S is the sign bit and X are the other bits.
Placing the binary point at
- 1 gives a range of -1.0 to 0.999999.
- 2 gives a range of -2.0 to 1.999999
- 3 gives a range of -4.0 to 3.999999 and so on.
When using different B scalings the complete B scaling formula must be used.
Consider a 32 bit word size, and two variables, one with a B scaling of 2 and the other with a scaling of 4.
1.4 @ B2 is 1.4 * (2wordsize-2-1)
1.4 * 2 ^ 29
0x2CCCCCCDNote that here the 1.4 values is very well represented with 30 fraction bits! A 32 bit real number
IEEE floating-point standard
IEEE 754–1985 was an industry standard for representingfloating-pointnumbers in computers, officially adopted in 1985 and superseded in 2008 byIEEE 754-2008. During its 23 years, it was the most widely used format for...
has 23 bits to store the fraction in. This is why B scaling is always more accurate than floating point of the same word size.
This is especially useful in integrator
Integrator
An integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
s or repeated summing of small quantities where rounding error can be a subtle but very dangerous problem, when using floating point.
Now a larger number 15.2 at B4.
15.2 @ B4 is 15.2 * (2 ^ (wordsize-4-1))
15.2 * 2 ^ 27
0x7999999AAgain the number of bits to store the fraction is 28 bits.
Multiplying these 32 bit numbers give the 64 bit result 0x1547AE14A51EB852
This result is in B7 in a 64 bit word. Shifting it down by 32 bits gives the result in B7 in 32 bits.
0x1547AE14
To convert back to floating point, divide this by (2^(wordsize-7-1))
21.2800000099
Various scalings maybe used. B0 for instance can be used to represent any number between -1 and 0.999999999.
Binary angles), −1.0 or 0.9999999 as 180 (or π) and −0.5 as 270 (or 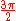). When these binary angles are added using normal two's complementTwo's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
mathematics the rotation of the angles is correct, even when crossing the sign boundary (this of course does away with checks for angle ≥ 360 when handling normal degrees).
The terms Binary Angular Measurement System (BAMS) and 'brads' (binary radians) refer to implementations of binary angles. They find use in robotics, navigation, computer games, digital sensors and weapons system's digital communications Binary angles may be thought of as the fractional part of an angle when expressed in units of turn
Turn (geometry)
A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
.
No matter what bit-pattern is stored in a binary angle, when it is multiplied by 360 (or 2π) using standard signed fixed-point arithmetic
Fixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
, the result is always a valid angle in the range of -180 degrees (-π radians) to +180 degrees (+π radians).
In some cases, it is convenient to use unsigned multiplication (rather than signed multiplication) on a binary angle, which gives the correct angle in the range of 0 to +360 degrees (+2π radians).
Compared to storing angles in a binary angle format, storing angles in any other format inevitably results in some bit patterns giving "angles" outside that range, requiring extra steps to range-reduce the value to the desired range, or results in some bit patterns that are not valid angles at all (NaN
NaN
In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
), or both.
Application of binary scaling techniques
Binary scaling techniques were used in the 1970s and 80s for real time computing that was mathematically intensive, such as flight simulation. The code was often commented with the binary scalings of the intermediate results of equations.
Binary scaling is still used in many DSP
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
applications and custom made microprocessors are usually based on binary scaling techniques.
Binary scaling is currently used in the DCT
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
used to compress JPEG
JPEG
In computing, JPEG . The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality....
images in utilities such as the GIMP
GIMP
GIMP is a free software raster graphics editor. It is primarily employed as an image retouching and editing tool and is freely available in versions tailored for most popular operating systems including Microsoft Windows, Apple Mac OS X, and Linux.In addition to detailed image retouching and...
.
Although floating point has taken over to a large degree, where speed and extra accuracy are required, binary scaling works on simpler hardware and is more accurate when the range of values is known in advance.