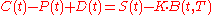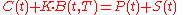Put–call parity
Encyclopedia
In financial mathematics, put–call parity defines a relationship between the price of a European call option and European put option in a frictionless market
—both with the identical strike price
and expiry, and the underlying being a liquid asset
. In the absence of liquidity, the existence of a forward contract
suffices. Put–call parity requires minimal assumptions and thus does not require assumptions such as those of Black–Scholes or other commonly used financial models.
can be any other trade-able asset. The ability to buy and sell the underlying is crucial to the "no arbitrage" argument below.
First, note that under the assumption that there are no arbitrage
opportunities, two portfolios that always have the same payoff at time T must have the same value at any prior time. To prove this suppose that, at some time t before T, one portfolio were cheaper than the other. Then one could purchase (go long) the cheaper portfolio and sell (go short) the more expensive. At time T, our overall portfolio would, for any value of the share price, have zero value (all the assets and liabilities have canceled out). The profit we made at time t is thus a riskless profit, but this violates our assumption of no arbitrage.
We will derive the put-call parity relation by creating two portfolios with the same payoffs and invoking the above principle.
Consider a call option and a put option with the same strike K for expiry at the same date T on some stock S, which pays no dividend. We assume the existence of a bond
that pays 1 dollar at maturity time T. The bond price may be random (like the stock) but must equal 1 at maturity.
Let the price of S be S(t) at time t. Now assemble a portfolio by buying a call option C and selling a put option P of the same maturity T and strike K. The payoff for this portfolio is S(T) - K. Now assemble a second portfolio by buying one share and borrowing K bonds. Note the payoff of the latter portfolio is also S(T) - K at time T, since our share bought for S(t) will be worth S(T) and the borrowed bonds will be worth K.
By our preliminary observation that identical payoffs imply that both portfolios must have the same price at a general time
, the following relationship exists between the value of the various instruments:
where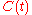
is the value of the call at time 
,
is the value of the put,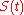
is the value of the share,
is the strike price, and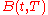
value of a bond that matures at time 
. If a stock pays dividends, they should be included in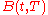 
, because option prices are typically not adjusted for ordinary dividends.
Note that the right-hand side of the equation is also the price of buying a forward contract
on the stock with delivery price K. Thus one way to read the equation is that a portfolio that is long a call and short a put is the same as being long a forward. In particular, if the underlying is not tradeable but there exists forwards on it, we can replace the right-hand-side expression by the price of a forward.
If the bond interest rate
,
, is assumed to be constant then
Thus given no arbitrage opportunities, the above relationship (put-call parity) holds, and for any three prices of the call, put, bond and stock one can compute the implied price of the fourth.
Note:
refers to the force of interest, which is approximately equal to the effective annual rate for small interest rates. However, one should take care with the approximation, especially with larger rates and larger time periods. To find 
exactly, use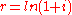 
, where 
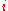is the effective annual interest rate.
When valuing European options written on stocks with known dividends that will be paid out during the life of the option, the formula becomes:
where D(t) represents the total value of the dividends from one stock share to be paid out over the remaining life of the options, discounted to present value
. This formula can be derived in similar manner to above, but with the modification that one portfolio consists of going long a call, going short a put, and D(T) bonds that each pay 1 dollar at maturity T (the bonds will be worth D(t) at time t); the other portfolio is the same as before - long one share of stock, short K bonds that each pay 1 dollar at T. The difference is that at time T, the stock is not only worth S(T) but has paid out D(T) in dividends.
We can rewrite the equation as:
and note that the right-hand side is the price of a forward contract on the stock with delivery price K, as before.
There is another way of thinking (and writing) the basic put-call relationship:
Both sides have payoff max(S(T), K) at time T, so this gives another way of proving put-call parity. The right-hand side is the value of a portfolio, a protective put, which is long a put and stock. The left-hand side is the value of a fiduciary call, which is long a call and enough bonds to buy a share of stock at time T if the call is exercised.
Michael Knoll, in The Ancient Roots of Modern Financial Innovation: The Early History of Regulatory Arbitrage, describes the important role that put-call parity played in developing the equity of redemption
, the defining characteristic of a modern mortgage, in Medieval England.
In the 19th century, financier Russell Sage
used put-call parity to create synthetic loans, which had higher interest rates than the usury laws of the time would have normally allowed.
Nelson, an option arbitrage trader in New York, published a book: "The A.B.C. of Options and Arbitrage" in 1904 that describes the put-call parity in detail. His book was re-discovered by Espen Gaarder Haug in the early 2000s and many references from Nelson's book are given in Haug's book "Derivatives Models on Models".
Henry Deutsch describes the put-call parity in 1910 in his book "Arbitrage in Bullion, Coins, Bills, Stocks, Shares and Options, 2nd Edition". London: Engham Wilson but in less detail than Nelson (1904).
Mathematics professor Vinzenz Bronzin
also derives the put-call parity in 1908 and uses it as part of his arbitrage argument to develop a series of mathematical option models under a series of different distributions. The work of professor Bronzin was just recently rediscovered by professor Wolfgang Hafner and professor Heinz Zimmermann. The original work of Bronzin is a book written in German and is now translated and published in English in an edited work by Hafner and Zimmermann ("Vinzenz Bronzin's option pricing models", Springer Verlag).
Its first description in the modern academic literature appears to be .
Frictionless market
A Frictionless market is a financial market without transaction costs. Friction is a type of market incompleteness. Every complete market is frictionless, but the converse does not hold. In a frictionless market the solvency cone is the halfspace normal to the unique price vector. The...
—both with the identical strike price
Strike price
In options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
and expiry, and the underlying being a liquid asset
Market liquidity
In business, economics or investment, market liquidity is an asset's ability to be sold without causing a significant movement in the price and with minimum loss of value...
. In the absence of liquidity, the existence of a forward contract
Forward contract
In finance, a forward contract or simply a forward is a non-standardized contract between two parties to buy or sell an asset at a specified future time at a price agreed today. This is in contrast to a spot contract, which is an agreement to buy or sell an asset today. It costs nothing to enter a...
suffices. Put–call parity requires minimal assumptions and thus does not require assumptions such as those of Black–Scholes or other commonly used financial models.
Derivation
We will suppose that the put and call options are on traded stocks, but the underlyingUnderlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
can be any other trade-able asset. The ability to buy and sell the underlying is crucial to the "no arbitrage" argument below.
First, note that under the assumption that there are no arbitrage
Arbitrage
In economics and finance, arbitrage is the practice of taking advantage of a price difference between two or more markets: striking a combination of matching deals that capitalize upon the imbalance, the profit being the difference between the market prices...
opportunities, two portfolios that always have the same payoff at time T must have the same value at any prior time. To prove this suppose that, at some time t before T, one portfolio were cheaper than the other. Then one could purchase (go long) the cheaper portfolio and sell (go short) the more expensive. At time T, our overall portfolio would, for any value of the share price, have zero value (all the assets and liabilities have canceled out). The profit we made at time t is thus a riskless profit, but this violates our assumption of no arbitrage.
We will derive the put-call parity relation by creating two portfolios with the same payoffs and invoking the above principle.
Consider a call option and a put option with the same strike K for expiry at the same date T on some stock S, which pays no dividend. We assume the existence of a bond
Bond (finance)
In finance, a bond is a debt security, in which the authorized issuer owes the holders a debt and, depending on the terms of the bond, is obliged to pay interest to use and/or to repay the principal at a later date, termed maturity...
that pays 1 dollar at maturity time T. The bond price may be random (like the stock) but must equal 1 at maturity.
Let the price of S be S(t) at time t. Now assemble a portfolio by buying a call option C and selling a put option P of the same maturity T and strike K. The payoff for this portfolio is S(T) - K. Now assemble a second portfolio by buying one share and borrowing K bonds. Note the payoff of the latter portfolio is also S(T) - K at time T, since our share bought for S(t) will be worth S(T) and the borrowed bonds will be worth K.
By our preliminary observation that identical payoffs imply that both portfolios must have the same price at a general time
, the following relationship exists between the value of the various instruments:
where
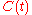is the value of the call at time , is the value of the put,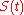 is the value of the share, is the strike price, and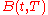 value of a bond that matures at time . If a stock pays dividends, they should be included in 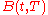, because option prices are typically not adjusted for ordinary dividends.Note that the right-hand side of the equation is also the price of buying a forward contract
Forward contract
In finance, a forward contract or simply a forward is a non-standardized contract between two parties to buy or sell an asset at a specified future time at a price agreed today. This is in contrast to a spot contract, which is an agreement to buy or sell an asset today. It costs nothing to enter a...
on the stock with delivery price K. Thus one way to read the equation is that a portfolio that is long a call and short a put is the same as being long a forward. In particular, if the underlying is not tradeable but there exists forwards on it, we can replace the right-hand-side expression by the price of a forward.
If the bond interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
,
, is assumed to be constant then
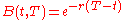
Thus given no arbitrage opportunities, the above relationship (put-call parity) holds, and for any three prices of the call, put, bond and stock one can compute the implied price of the fourth.
Note:
refers to the force of interest, which is approximately equal to the effective annual rate for small interest rates. However, one should take care with the approximation, especially with larger rates and larger time periods. To find exactly, use 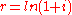, where 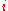is the effective annual interest rate.When valuing European options written on stocks with known dividends that will be paid out during the life of the option, the formula becomes:
where D(t) represents the total value of the dividends from one stock share to be paid out over the remaining life of the options, discounted to present value
Present value
Present value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...
. This formula can be derived in similar manner to above, but with the modification that one portfolio consists of going long a call, going short a put, and D(T) bonds that each pay 1 dollar at maturity T (the bonds will be worth D(t) at time t); the other portfolio is the same as before - long one share of stock, short K bonds that each pay 1 dollar at T. The difference is that at time T, the stock is not only worth S(T) but has paid out D(T) in dividends.
We can rewrite the equation as:
and note that the right-hand side is the price of a forward contract on the stock with delivery price K, as before.
There is another way of thinking (and writing) the basic put-call relationship:
Both sides have payoff max(S(T), K) at time T, so this gives another way of proving put-call parity. The right-hand side is the value of a portfolio, a protective put, which is long a put and stock. The left-hand side is the value of a fiduciary call, which is long a call and enough bonds to buy a share of stock at time T if the call is exercised.
History
Forms of put-call parity appeared in practice as early as medieval ages, and was formally described by a number of authors in the early 20th century.Michael Knoll, in The Ancient Roots of Modern Financial Innovation: The Early History of Regulatory Arbitrage, describes the important role that put-call parity played in developing the equity of redemption
Equity of redemption
The equity of redemption refers to the right of a mortgagor in law to redeem his property once the liability secured by the mortgage has been discharged.-Overview:...
, the defining characteristic of a modern mortgage, in Medieval England.
In the 19th century, financier Russell Sage
Russell Sage
Russell Sage was a financier, railroad executive and Whig politician from New York, United States. As a frequent partner of Jay Gould in various transactions, he amassed a fortune, which passed to his second wife, Margaret Olivia Slocum Sage, when he died...
used put-call parity to create synthetic loans, which had higher interest rates than the usury laws of the time would have normally allowed.
Nelson, an option arbitrage trader in New York, published a book: "The A.B.C. of Options and Arbitrage" in 1904 that describes the put-call parity in detail. His book was re-discovered by Espen Gaarder Haug in the early 2000s and many references from Nelson's book are given in Haug's book "Derivatives Models on Models".
Henry Deutsch describes the put-call parity in 1910 in his book "Arbitrage in Bullion, Coins, Bills, Stocks, Shares and Options, 2nd Edition". London: Engham Wilson but in less detail than Nelson (1904).
Mathematics professor Vinzenz Bronzin
Vinzenz Bronzin
Vinzenz Bronzin was a professor of mathematics in Trieste, Italy. Bronzin developed an early option pricing formula which was similar to the later Black–Scholes formula.- Publications :* Bronzin, V: Theorie der Prämiengeschäfte ;...
also derives the put-call parity in 1908 and uses it as part of his arbitrage argument to develop a series of mathematical option models under a series of different distributions. The work of professor Bronzin was just recently rediscovered by professor Wolfgang Hafner and professor Heinz Zimmermann. The original work of Bronzin is a book written in German and is now translated and published in English in an edited work by Hafner and Zimmermann ("Vinzenz Bronzin's option pricing models", Springer Verlag).
Its first description in the modern academic literature appears to be .
Implications
Put–call parity implies:- Equivalence of calls and puts: Parity implies that a call and a put can be used interchangeably in any delta-neutralDelta neutralIn finance, delta neutral describes a portfolio of related financial securities, in which the portfolio value remains unchanged due to small changes in the value of the underlying security...
portfolio. If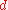
is the call's delta, then buying a call, and selling 
shares of stock, is the same as buying a put and buying 
shares of stock. Equivalence of calls and puts is very important when trading options.
- Parity of implied volatility: In the absence of dividends or other costs of carry (such as when a stock is difficult to borrow or sell short), the implied volatilityImplied volatilityIn financial mathematics, the implied volatility of an option contract is the volatility of the price of the underlying security that is implied by the market price of the option based on an option pricing model. In other words, it is the volatility that, when used in a particular pricing model,...
of calls and puts must be identical.
External links
- Put-Call parity
- Put-Call Parity and Arbitrage Opportunity, investopedia.com
- The Ancient Roots of Modern Financial Innovation: The Early History of Regulatory Arbitrage, Michael Knoll's history of Put-Call Parity
- Other abitrage relationships
- Arbitrage Relationships for Options, Prof. Thayer Watkins
- Rational Rules and Boundary Conditions for Option Pricing (PDFDiPortable Document FormatPortable Document Format is an open standard for document exchange. This file format, created by Adobe Systems in 1993, is used for representing documents in a manner independent of application software, hardware, and operating systems....
), Prof. Don M. Chance - No-Arbitrage Bounds on Options, Prof. Robert Novy-Marx
- Tools
- Option Arbitrage Relations, Prof. Campbell R. Harvey