Pseudoholomorphic curve
Encyclopedia
In mathematics
, specifically in topology
and geometry
, a pseudoholomorphic curve (or J-holomorphic curve) is a smooth map from a Riemann surface
into an almost complex manifold
that satisfies the Cauchy–Riemann equation. Introduced in 1985 by Mikhail Gromov, pseudoholomorphic curves have since revolutionized the study of symplectic manifold
s. In particular, they lead to the Gromov–Witten invariants and Floer homology
, and play a prominent role in string theory
.
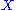be an almost complex manifold with almost complex structure 
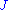. Let 
be a smooth Riemann surface
(also called a complex curve
) with complex structure
. A pseudoholomorphic curve in 
is a map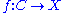 
that satisfies the Cauchy–Riemann equation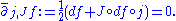
Since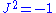
, this condition is equivalent to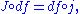
which simply means that the differential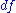
is complex-linear, that is, 
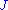maps each tangent space
to itself. For technical reasons, it is often preferable to introduce some sort of inhomogeneous term
and to study maps satisfying the perturbed Cauchy–Riemann equation
A pseudoholomorphic curve satisfying this equation can be called, more specifically, a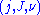
-holomorphic curve. The perturbation 
is sometimes assumed to be generated by a Hamiltonian
(particularly in Floer theory), but in general it need not be.
A pseudoholomorphic curve is, by its definition, always parametrized. In applications one is often truly interested in unparametrized curves, meaning embedded (or immersed) two-submanifolds of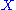
, so one mods out by reparametrizations of the domain that preserve the relevant structure. In the case of Gromov-Witten invariants, for example, we consider only closed
domains
of fixed genus 
and we introduce 
marked points (or punctures) on 
. As soon as the punctured Euler characteristic
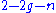is negative, there are only finitely many holomorphic reparametrizations of 
that preserve the marked points. The domain curve 
is an element of the Deligne–Mumford moduli space of curves.
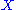and 
are both simply the complex number
plane. In real coordinates
and
where
. After multiplying these matrices in two different orders, one sees immediately that the equation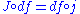
written above is equivalent to the classical Cauchy–Riemann equations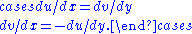
interacts with a symplectic form 
. An almost complex structure 
is said to be 
-tame if and only if
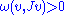
for all nonzero tangent vectors
. Tameness implies that the formula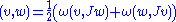
defines a Riemannian metric on
. Gromov showed that, for a given 
, the space of 
-tame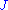 
is nonempty and contractible. He used this theory to prove a nonsqueezing theorem
concerning symplectic embeddings of spheres into cylinders.
Gromov showed that certain moduli space
s of pseudoholomorphic curves (satisfying additional specified conditions) are compact
, and described the way in which pseudoholomorphic curves can degenerate when only finite energy is assumed. (The finite energy condition holds most notably for curves with a fixed homology class in a symplectic manifold where J is
-tame or 
-compatible). This Gromov compactness theorem, now greatly generalized using stable map
s, makes possible the definition of Gromov-Witten invariants, which count pseudoholomorphic curves in symplectic manifolds.
Compact moduli spaces of pseudoholomorphic curves are also used to construct Floer homology
, which Andreas Floer
(and later authors, in greater generality) used to prove the famous conjecture of Vladimir Arnol'd concerning the number of fixed points of Hamiltonian flows.
of quantum mechanics
, one wishes to compute certain integrals over the space of all such surfaces. Because such a space is infinite-dimensional, these path integrals are not mathematically well-defined in general. However, under the A-twist one can deduce that the surfaces are parametrized by pseudoholomorphic curves, and so the path integrals reduce to integrals over moduli spaces of pseudoholomorphic curves (or rather stable maps), which are finite-dimensional. In closed type IIA string theory, for example, these integrals are precisely the Gromov-Witten invariant
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a pseudoholomorphic curve (or J-holomorphic curve) is a smooth map from a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
into an almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
that satisfies the Cauchy–Riemann equation. Introduced in 1985 by Mikhail Gromov, pseudoholomorphic curves have since revolutionized the study of symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s. In particular, they lead to the Gromov–Witten invariants and Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
, and play a prominent role in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
Definition
Let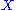 be an almost complex manifold with almost complex structure 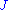. Let be a smooth Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
(also called a complex curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
) with complex structure
. A pseudoholomorphic curve in is a map 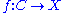that satisfies the Cauchy–Riemann equation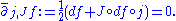Since
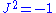, this condition is equivalent to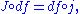which simply means that the differential
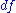is complex-linear, that is, 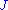maps each tangent spaceto itself. For technical reasons, it is often preferable to introduce some sort of inhomogeneous term
and to study maps satisfying the perturbed Cauchy–Riemann equationA pseudoholomorphic curve satisfying this equation can be called, more specifically, a
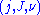-holomorphic curve. The perturbation is sometimes assumed to be generated by a HamiltonianHamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
(particularly in Floer theory), but in general it need not be.
A pseudoholomorphic curve is, by its definition, always parametrized. In applications one is often truly interested in unparametrized curves, meaning embedded (or immersed) two-submanifolds of
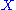, so one mods out by reparametrizations of the domain that preserve the relevant structure. In the case of Gromov-Witten invariants, for example, we consider only closedClosed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
domains
of fixed genus and we introduce marked points (or punctures) on . As soon as the punctured Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
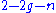is negative, there are only finitely many holomorphic reparametrizations of that preserve the marked points. The domain curve is an element of the Deligne–Mumford moduli space of curves.Analogy with the classical Cauchy–Riemann equations
The classical case occurs when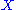 and are both simply the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane. In real coordinates
and
where
. After multiplying these matrices in two different orders, one sees immediately that the equation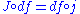written above is equivalent to the classical Cauchy–Riemann equations
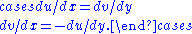
Applications in symplectic topology
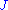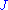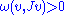
Although they can be defined for any almost complex manifold, pseudoholomorphic curves are especially interesting when interacts with a symplectic form . An almost complex structure is said to be -tame if and only iffor all nonzero tangent vectors
. Tameness implies that the formula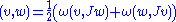defines a Riemannian metric on
. Gromov showed that, for a given , the space of -tame is nonempty and contractible. He used this theory to prove a nonsqueezing theoremNonsqueezing theorem
The nonsqueezing theorem is one of the most important theorems in symplectic geometry. It was first proven by Mikhail Gromov in 1985. The theorem states that one cannot embed a sphere into a cylinder via a symplectic map unless the radius of the sphere is less than or equal to the radius of the...
concerning symplectic embeddings of spheres into cylinders.
Gromov showed that certain moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s of pseudoholomorphic curves (satisfying additional specified conditions) are compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, and described the way in which pseudoholomorphic curves can degenerate when only finite energy is assumed. (The finite energy condition holds most notably for curves with a fixed homology class in a symplectic manifold where J is
-tame or -compatible). This Gromov compactness theorem, now greatly generalized using stable mapStable map
In mathematics, specifically in symplectic topology and algebraic geometry, one can construct the moduli space of stable maps, satisfying specified conditions, from Riemann surfaces into a given symplectic manifold. This moduli space is the essence of the Gromov–Witten invariants, which find...
s, makes possible the definition of Gromov-Witten invariants, which count pseudoholomorphic curves in symplectic manifolds.
Compact moduli spaces of pseudoholomorphic curves are also used to construct Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
, which Andreas Floer
Andreas Floer
Andreas Floer was a German mathematician who made seminal contributions to the areas of geometry, topology, and mathematical physics, in particular the invention of Floer homology.-Life:...
(and later authors, in greater generality) used to prove the famous conjecture of Vladimir Arnol'd concerning the number of fixed points of Hamiltonian flows.
Applications in physics
In type II string theory, one considers surfaces traced out by strings as they travel along paths in a Calabi-Yau 3-fold. Following the path integral formulationPath integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, one wishes to compute certain integrals over the space of all such surfaces. Because such a space is infinite-dimensional, these path integrals are not mathematically well-defined in general. However, under the A-twist one can deduce that the surfaces are parametrized by pseudoholomorphic curves, and so the path integrals reduce to integrals over moduli spaces of pseudoholomorphic curves (or rather stable maps), which are finite-dimensional. In closed type IIA string theory, for example, these integrals are precisely the Gromov-Witten invariant
Gromov-Witten invariant
In mathematics, specifically in symplectic topology and algebraic geometry, Gromov–Witten invariants are rational numbers that, in certain situations, count pseudoholomorphic curves meeting prescribed conditions in a given symplectic manifold...
s.