Prüfer sequence
Encyclopedia
In combinatorial
mathematics
, the Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled tree is a unique sequence
associated with the tree. The sequence for a tree on n vertices has length n − 2, and can be generated by a simple iterative algorithm. Prüfer sequences were first used by Heinz Prüfer
to prove Cayley's formula in 1918.
The Prüfer sequence of a labeled tree is unique up to isomorphism
and has length n − 2.
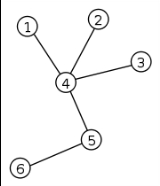
Consider the above algorithm run on the tree shown to the right. Initially, vertex 1 is the leaf with the smallest label, so it is removed first and 4 is put in the Prüfer sequence. Vertices 2 and 3 are removed next, so 4 is added twice more. Vertex 4 is now a leaf and has the smallest label, so it is removed and we append 5 to the sequence. We are left with only two vertices, so we stop. The tree's sequence is {4,4,4,5}.
The tree will have
For each node set its degree to the number of times it appears in the sequence plus 1.
For instance, in pseudo-code:
Convert-Prüfer-to-Tree(a)
1 n ← length[a]
2 T ← a graph with n + 2 isolated nodes, numbered 1 to n + 2
3 degree ← an array of integers
4 for each node i in T
5 do degree[i] ← 1
6 for each value i in a
7 do degree[i] ← degree[i] + 1
Next, for each number in the sequence
7 for each value i in a
8 for each node j in T
9 if degree[j] = 1
10 then Insert edge[i, j] into T
11 degree[i] ← degree[i] - 1
12 degree[j] ← degree[j] - 1
13 break
At the end of this loop two nodes with degree 1 will remain (call them
14 u ← v ← 0
15 for each node i in T
16 if degree[i] = 1
17 then if u = 0
18 then u ← i
19 else v ← i
20 break
21 Insert edge[u, v] into T
22 degree[u] ← degree[u] - 1
23 degree[v] ← degree[v] - 1
24 return T
The immediate consequence is that Prüfer sequences provide a bijection
between the set of labeled trees on n vertices and the set of sequences of length n–2 on the labels 1 to n. The latter set has size nn−2, so the existence of this bijection proves Cayley's formula, i.e. that there are
nn−2 labeled trees on n vertices.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled tree is a unique sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
associated with the tree. The sequence for a tree on n vertices has length n − 2, and can be generated by a simple iterative algorithm. Prüfer sequences were first used by Heinz Prüfer
Heinz Prüfer
Ernst Paul Heinz Prüfer was a German mathematician, who worked on abelian groups, algebraic numbers, knot theory and Sturm-Liouville theory. His advisor was Issai Schur.- See also :* Prüfer manifold...
to prove Cayley's formula in 1918.
Algorithm to convert a tree into a Prüfer sequence
One can generate a labeled tree's Prüfer sequence by iteratively removing vertices from the tree until only two vertices remain. Specifically, consider a labeled tree T with vertices {1, 2, ..., n}. At step i, remove the leaf with the smallest label and set the ith element of the Prüfer sequence to be the label of this leaf's neighbour.The Prüfer sequence of a labeled tree is unique up to isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
and has length n − 2.
Example
Algorithm to convert a Prüfer sequence into a tree
Let{a[1], a[2], ..., a[n]} be a Prüfer sequence:The tree will have
n+2 nodes, numbered from 1 to n+2.For each node set its degree to the number of times it appears in the sequence plus 1.
For instance, in pseudo-code:
Convert-Prüfer-to-Tree(a)
1 n ← length[a]
2 T ← a graph with n + 2 isolated nodes, numbered 1 to n + 2
3 degree ← an array of integers
4 for each node i in T
5 do degree[i] ← 1
6 for each value i in a
7 do degree[i] ← degree[i] + 1
Next, for each number in the sequence
a[i], find the first (lowest-numbered) node, j, with degree equal to 1, add the edge (j, a[i]) to the tree, and decrement the degrees of j and a[i]. In pseudo-code:7 for each value i in a
8 for each node j in T
9 if degree[j] = 1
10 then Insert edge[i, j] into T
11 degree[i] ← degree[i] - 1
12 degree[j] ← degree[j] - 1
13 break
At the end of this loop two nodes with degree 1 will remain (call them
u, v). Lastly, add the edge (u,v) to the tree.14 u ← v ← 0
15 for each node i in T
16 if degree[i] = 1
17 then if u = 0
18 then u ← i
19 else v ← i
20 break
21 Insert edge[u, v] into T
22 degree[u] ← degree[u] - 1
23 degree[v] ← degree[v] - 1
24 return T
Cayley's formula
The Prüfer sequence of a labeled tree on n vertices is a unique sequence of length n − 2 on the labels 1 to n — this much is clear. Somewhat less obvious is the fact that for a given sequence S of length n–2 on the labels 1 to n, there is a unique labeled tree whose Prüfer sequence is S.The immediate consequence is that Prüfer sequences provide a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the set of labeled trees on n vertices and the set of sequences of length n–2 on the labels 1 to n. The latter set has size nn−2, so the existence of this bijection proves Cayley's formula, i.e. that there are
nn−2 labeled trees on n vertices.
Other applications
- Cayley's formula can be strengthened to prove the following claim:
- The number of spanning trees in a complete graph
with degrees 
is equal to
- The proof follows by observing that in the Prüfer sequence number
appears exactly 
times.
- Cayley's formula can be generalized: a labeled tree is in fact a spanning treeSpanning tree (mathematics)In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of the labeled complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. By placing restrictions on the enumerated Prüfer sequences, similar methods can give the number of spanning trees of a complete bipartite graphBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. If G is the complete bipartite graph with vertices 1 to n1 in one partition and vertices n1 + 1 to n in the other partition, the number of labeled spanning trees of G is
, where n2 = n − n1.
External links
- Prüfer code – from MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...