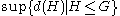Prüfer rank
Encyclopedia
In mathematics
, especially in the area of algebra
known as group theory
, the Prüfer rank of a pro-p group
measures the size of a group in terms of the ranks of its elementary abelian
section
s. The rank is well behaved and helps to define analytic pro-p-groups. The term is named after Heinz Prüfer
.
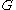is
where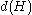
is the rank
of the abelian group
,
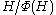where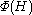
is the Frattini subgroup
of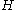
.
As the Frattini subgroup of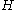
can be thought of as the group of non-generating elements of 
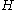, it can be seen that 
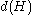will be equal to the size of any minimal generating set of 
.
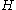Specifically in the case of finitely generated pro-p group
s, having finite Prüfer rank is equivalent to having an open
normal subgroup
that is powerful. In turn these are precisely the class of pro-p group
s that are p-adic
analytic - that is groups that can be imbued with a
p-adic
manifold
structure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Prüfer rank of a pro-p group
Pro-p group
In mathematics, a pro-p group is a profinite group G such that for any open normal subgroup N\triangleleft G the quotient group G/N is a p-group...
measures the size of a group in terms of the ranks of its elementary abelian
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
section
Section (group theory)
In group theory a section of a group G is a group that is, or is isomorphic to, a quotient group of a subgroup of G.- Examples :Of the 26 sporadic groups, 20 are sections of the monster group, and are referred to as the "Happy Family"....
s. The rank is well behaved and helps to define analytic pro-p-groups. The term is named after Heinz Prüfer
Heinz Prüfer
Ernst Paul Heinz Prüfer was a German mathematician, who worked on abelian groups, algebraic numbers, knot theory and Sturm-Liouville theory. His advisor was Issai Schur.- See also :* Prüfer manifold...
.
Definition
The Prüfer rank of pro-p-group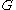 is
where
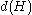is the rankRank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
of the abelian group
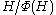,where
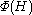is the Frattini subgroupFrattini subgroup
In mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
of
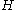.As the Frattini subgroup of
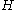can be thought of as the group of non-generating elements of 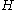, it can be seen that 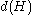will be equal to the size of any minimal generating set of 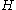.Properties
Those profinite groups with finite Prüfer rank are more amenable to analysis.Specifically in the case of finitely generated pro-p group
Pro-p group
In mathematics, a pro-p group is a profinite group G such that for any open normal subgroup N\triangleleft G the quotient group G/N is a p-group...
s, having finite Prüfer rank is equivalent to having an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
that is powerful. In turn these are precisely the class of pro-p group
Pro-p group
In mathematics, a pro-p group is a profinite group G such that for any open normal subgroup N\triangleleft G the quotient group G/N is a p-group...
s that are p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
analytic - that is groups that can be imbued with a
p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
structure.