
Proof complexity
Encyclopedia
In computer science
, proof complexity is a measure of efficiency of automated theorem proving
methods that is based on the size of the proofs they produce. The methods for proving contradiction in propositional logic are the most analyzed. The two main issues considered in proof complexity are whether a proof method can produce a polynomial proof of every inconsistent formula, and whether the proofs produced by one method are always of size similar to those produced by another method.
for theorem proving in propositional logic, such as the sequent calculus
, the cutting-plane method
, resolution
, the DPLL algorithm
, etc. produce different proofs when applied to the same formula. Proof complexity measures the efficiency of a method in terms of the size of the proofs it produces.
Two points make the study of proof complexity non-trivial:
The first point is taken into account by comparing the size of a proof of a formula with the size of the formula. This comparison is made using the usual assumptions of computational complexity
: first, a polynomial proof size/formula size ratio means that the proof is of size similar to that of the formula; second, this ratio is studied in the asymptotic case as the size of the formula increases.
The second point is taken into account by considering, for each formula, the shortest possible proof the considered method can produce.
The question of polynomiality of proofs is whether a method can always produce a proof of size polynomial in the size of the formula. If such a method exists, then NP
would be equal to coNP: this is why the question of polynomiality of proofs is considered important in computational complexity. For some methods, the existence of formulae whose shortest proofs are always superpolynomial has been proved. For other methods, it is an open question.
When comparing two proof methods, two outcomes are possible:
Several proofs of the second kind involve contradictory formulae expressing the negation of the pigeonhole principle, namely that pigeons can fit
pigeons can fit  holes with no hole containing two or more pigeons.
holes with no hole containing two or more pigeons.
does not collapses, which would happen if generating a proof in time polynomial in the size of the formula were always possible.
 . The tautology is true for every choice of
. The tautology is true for every choice of 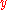 , and after fixing
, and after fixing 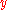 the evaluation of
the evaluation of  and
and  are independent because are defined on disjoint sets of variables. This means that it is possible to define an interpolant circuit
are independent because are defined on disjoint sets of variables. This means that it is possible to define an interpolant circuit 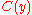 , such that both
, such that both  and
and 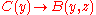 hold. The interpolant circuit decides either if
hold. The interpolant circuit decides either if 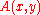 is false or if
is false or if 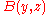 is true, by only considering
is true, by only considering 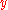 . The nature of the interpolant circuit can be arbitrary. Nevertheless it is possible to use a proof of the initial tautology
. The nature of the interpolant circuit can be arbitrary. Nevertheless it is possible to use a proof of the initial tautology  as a hint on how to construct
as a hint on how to construct  . Some proof systems (e.g. resolution) are said to have efficient interpolation because the interpolant
. Some proof systems (e.g. resolution) are said to have efficient interpolation because the interpolant 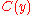 is efficiently computable from any proof of the tautology
is efficiently computable from any proof of the tautology  in such proof system. The efficiency is measured with respect to the length of the proof: it is easier to compute interpolants for longer proofs, so this property seems to be anti-monotone in the strength of the proof system.
in such proof system. The efficiency is measured with respect to the length of the proof: it is easier to compute interpolants for longer proofs, so this property seems to be anti-monotone in the strength of the proof system.
Interpolation is a weak form of automatization: a way to deduce the existence of small circuits from the existence of small proofs. In particular the following three statements cannot be simultaneously true: (a) has a short proof in a some proof system; (b) such proof system has efficient interpolation; (c) the interpolant circuit solves a computationally hard problem. It is clear that (a) and (b) imply that there is a small interpolant circuit, which is in contradiction with (c). Such relation allows to turn proof length upper bounds into lower bounds on computations, and dually to turn efficient interpolation algorithms into lower bounds on proof length.
has a short proof in a some proof system; (b) such proof system has efficient interpolation; (c) the interpolant circuit solves a computationally hard problem. It is clear that (a) and (b) imply that there is a small interpolant circuit, which is in contradiction with (c). Such relation allows to turn proof length upper bounds into lower bounds on computations, and dually to turn efficient interpolation algorithms into lower bounds on proof length.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, proof complexity is a measure of efficiency of automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
methods that is based on the size of the proofs they produce. The methods for proving contradiction in propositional logic are the most analyzed. The two main issues considered in proof complexity are whether a proof method can produce a polynomial proof of every inconsistent formula, and whether the proofs produced by one method are always of size similar to those produced by another method.
Polynomiality of proofs
Different propositional proof systemPropositional proof system
In propositional calculus and proof complexity a propositional proof system , also called a Cook–Reckhow propositional proof system, is system for proving classical propositional tautologies.- Mathematical definition :...
for theorem proving in propositional logic, such as the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, the cutting-plane method
Cutting-plane method
In mathematical optimization, the cutting-plane method is an umbrella term for optimization methods which iteratively refine a feasible set or objective function by means of linear inequalities, termed cuts...
, resolution
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
, the DPLL algorithm
DPLL algorithm
The Davis–Putnam–Logemann–Loveland algorithm is a complete, backtracking-based algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem....
, etc. produce different proofs when applied to the same formula. Proof complexity measures the efficiency of a method in terms of the size of the proofs it produces.
Two points make the study of proof complexity non-trivial:
- the size of a proof depends on the formula that is to be proved inconsistent;
- proof methods are generally families of algorithms, as some of their steps are not univocally specified; for example, resolution is based on iteratively choosing a pair of clauses containing opposite literals and producing a new clause that is a consequence of them; since several such pairs may be available at each step, the algorithm has to choose one; these choices affect the proof length.
The first point is taken into account by comparing the size of a proof of a formula with the size of the formula. This comparison is made using the usual assumptions of computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
: first, a polynomial proof size/formula size ratio means that the proof is of size similar to that of the formula; second, this ratio is studied in the asymptotic case as the size of the formula increases.
The second point is taken into account by considering, for each formula, the shortest possible proof the considered method can produce.
The question of polynomiality of proofs is whether a method can always produce a proof of size polynomial in the size of the formula. If such a method exists, then NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
would be equal to coNP: this is why the question of polynomiality of proofs is considered important in computational complexity. For some methods, the existence of formulae whose shortest proofs are always superpolynomial has been proved. For other methods, it is an open question.
Proof size comparison
A second question about proof complexity is whether a method is more efficient than another. Since the proof size depends on the formula, it is possible that one method can produce a short proof of a formula and only long proofs of another formula, while a second method can have exactly the opposite behavior. The assumptions of measuring the size of the proofs relative to the size of the formula and considering only the shortest proofs are also used in this context.When comparing two proof methods, two outcomes are possible:
- for every proof of a formula produced using the first method, there is a proof of comparable size of the same formula produced by the second method;
- there exists a formula such that the first method can produce a short proof while all proofs obtained by the second method are consistently larger.
Several proofs of the second kind involve contradictory formulae expressing the negation of the pigeonhole principle, namely that
 pigeons can fit
pigeons can fit  holes with no hole containing two or more pigeons.
holes with no hole containing two or more pigeons.Automatizability
A proof method is automatizable if one of the shorter proofs of a formula can always be generated in time polynomial (or sub-exponential) in the size of the proof. Some methods, but not all, are automatizable. Automatizability results are not in contrast with the assumption that the polynomial hierarchyPolynomial hierarchy
In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines...
does not collapses, which would happen if generating a proof in time polynomial in the size of the formula were always possible.
Interpolation
Consider a tautology of the form . The tautology is true for every choice of
. The tautology is true for every choice of 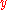 , and after fixing
, and after fixing 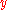 the evaluation of
the evaluation of  and
and  are independent because are defined on disjoint sets of variables. This means that it is possible to define an interpolant circuit
are independent because are defined on disjoint sets of variables. This means that it is possible to define an interpolant circuit 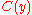 , such that both
, such that both  and
and 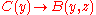 hold. The interpolant circuit decides either if
hold. The interpolant circuit decides either if 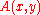 is false or if
is false or if 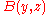 is true, by only considering
is true, by only considering 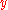 . The nature of the interpolant circuit can be arbitrary. Nevertheless it is possible to use a proof of the initial tautology
. The nature of the interpolant circuit can be arbitrary. Nevertheless it is possible to use a proof of the initial tautology  as a hint on how to construct
as a hint on how to construct  . Some proof systems (e.g. resolution) are said to have efficient interpolation because the interpolant
. Some proof systems (e.g. resolution) are said to have efficient interpolation because the interpolant 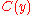 is efficiently computable from any proof of the tautology
is efficiently computable from any proof of the tautology  in such proof system. The efficiency is measured with respect to the length of the proof: it is easier to compute interpolants for longer proofs, so this property seems to be anti-monotone in the strength of the proof system.
in such proof system. The efficiency is measured with respect to the length of the proof: it is easier to compute interpolants for longer proofs, so this property seems to be anti-monotone in the strength of the proof system.Interpolation is a weak form of automatization: a way to deduce the existence of small circuits from the existence of small proofs. In particular the following three statements cannot be simultaneously true: (a)
 has a short proof in a some proof system; (b) such proof system has efficient interpolation; (c) the interpolant circuit solves a computationally hard problem. It is clear that (a) and (b) imply that there is a small interpolant circuit, which is in contradiction with (c). Such relation allows to turn proof length upper bounds into lower bounds on computations, and dually to turn efficient interpolation algorithms into lower bounds on proof length.
has a short proof in a some proof system; (b) such proof system has efficient interpolation; (c) the interpolant circuit solves a computationally hard problem. It is clear that (a) and (b) imply that there is a small interpolant circuit, which is in contradiction with (c). Such relation allows to turn proof length upper bounds into lower bounds on computations, and dually to turn efficient interpolation algorithms into lower bounds on proof length.Non-classical logics
The idea of comparing the size of proofs can be used for any automated reasoning procedure that generates a proof. Some research has been done about the size of proofs for propositional non-classical logics, in particular, intuitionistic, modal, and non-monotonic logics.See also
- Automated theorem provingAutomated theorem provingAutomated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
- Computational complexityComputational ComplexityComputational Complexity may refer to:*Computational complexity theory*Computational Complexity...
- Intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
- Non-monotonic logicNon-monotonic logicA non-monotonic logic is a formal logic whose consequence relation is not monotonic. Most studied formal logics have a monotonic consequence relation, meaning that adding a formula to a theory never produces a reduction of its set of consequences. Intuitively, monotonicity indicates that learning a...

