
Primality certificate
Encyclopedia
In mathematics
and computer science
, a primality certificate or primality proof is a succinct, formal proof that a number is prime. Primality certificates allow the primality of a number to be rapidly checked without having to run an expensive or unreliable primality test
. By "succinct", we usually mean that we wish for the proof to be at most polynomially larger than the number of digits in the number itself (for example, if the number has b bits, the proof might contain roughly b2 bits).
Primality certificates lead directly to proofs that problems such as primality testing and the complement
of integer factorization
lie in NP
, the class of problems verifiable in polynomial time given a solution. These problems already trivially lie in co-NP. This was the first strong evidence that these problems are not NP-complete
, since if they were it would imply NP = co-NP, a result widely believed to be false; in fact, this was the first demonstration of a problem in NP intersect co-NP not known (at the time) to be in P.
Producing certificates for the complement problem, to establish that a number is composite, is straightforward; it suffices to give a nontrivial divisor. Standard probabilistic primality tests such as the Fermat primality test
and the Miller-Rabin primality test
also produce compositeness certificates in the event where the input is composite, but do not produce certificates for prime inputs.
with an added condition to make it true:
Given such an a (called a witness) and the prime factorization of n−1, it's simple to verify the above conditions quickly: we only need to do a linear number of modular exponentiations, since every integer has fewer prime factors than bits, and each of these can be done by exponentiation by squaring
in O(log n) multiplications (see big-O notation). Even with grade-school integer multiplication, this is only O((log n)4) time; using the multiplication algorithm
with best-known asymptotic running time, the Schönhage–Strassen algorithm, we can lower this to O((log n)3(log log n)(log log log n)) time, or using soft-O notation Õ((log n)3).
However, it is possible to trick a verifier into accepting a composite number by giving it a "prime factorization" of n−1 that includes composite numbers. For example, suppose we claim that n=85 is prime, supplying a=4 and n−1=6×14 as the "prime factorization". Then (using q=6 and q=14):
We would falsely conclude that 85 is prime. We don't want to just force the verifier to factor the number, because there is no known general polynomial-time factoring algorithm.
A better way to avoid this issue is to give primality certificates for each of the prime factors of n−1 as well, which are just smaller instances of the original problem. We continue recursively in this manner until we reach a number known to be prime, such as 2. We end up with a tree of prime numbers, each associated with a witness a. For example, here is a complete Pratt certificate for the number 229:
This proof tree can be shown to contain at most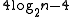 values other than 2 by a simple inductive proof (based on Theorem 2 of Pratt). The result holds for 3; in general, take p > 3 and let its children in the tree be p1,...,pk. By the inductive hypothesis the tree rooted at pi contains at most
values other than 2 by a simple inductive proof (based on Theorem 2 of Pratt). The result holds for 3; in general, take p > 3 and let its children in the tree be p1,...,pk. By the inductive hypothesis the tree rooted at pi contains at most 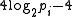 values, so the entire tree contains at most:
values, so the entire tree contains at most:
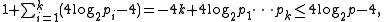
since k ≥ 2 and p1...pk = p−1. Since each value has at most log n bits, this also demonstrates that the certificate has a size of O((log n)2) bits.
Since there are O(log n) values other than 2 and each requires at most one exponentiation to verify (and exponentiations dominate the running time), the total time is O((log n)3(log log n)(log log log n)) or Õ((log n)3), which is quite feasible for numbers in the range that computational number theorists usually work with.
However, while useful in theory and easy to verify, actually generating a Pratt certificate for n requires factoring n−1 and other potentially large numbers. This is simple for some special numbers such as Fermat primes, but currently much more difficult than simple primality testing for large primes of general form.
and Joe Kilian described a new type of certificate based on the theory of elliptic curve
s. This was in turn used by A. O. L. Atkin
and François Morain as the basis for Atkin-Goldwasser-Kilian-Morain certificates, which are the type of certificates generated and verified by elliptic curve primality proving
systems. Just as Pratt certificates are based on Lehmer's theorem, Atkin-Goldwasser-Kilian-Morain certificates are based on the following theorem of Goldwasser and Kilian (Lemma 2 of "Almost All Primes Can Be Quickly Certified"):
Technically, an elliptic curve can only be constructed over a field, and is only a field if n is prime, so we seem to be assuming the result we're trying to prove. The difficulty arises in the elliptic curve addition algorithm, which takes inverses in the field that may not exist in
is only a field if n is prime, so we seem to be assuming the result we're trying to prove. The difficulty arises in the elliptic curve addition algorithm, which takes inverses in the field that may not exist in 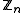 . However, it can be shown (Lemma 1 of "Almost All Primes Can Be Quickly Certified") that if we merely perform computations as though the curve were well-defined and do not at any point attempt to invert an element with no inverse, the result is still valid; if we do encounter an element with no inverse, this establishes that n is composite.
. However, it can be shown (Lemma 1 of "Almost All Primes Can Be Quickly Certified") that if we merely perform computations as though the curve were well-defined and do not at any point attempt to invert an element with no inverse, the result is still valid; if we do encounter an element with no inverse, this establishes that n is composite.
To derive a certificate from this theorem, we first encode Mx, My, A, B, and q, then recursively encode the proof of primality for q < n, continuing until we reach a known prime. This certificate has size O((log n)2) and can be verified in O((log n)4) time. Moreover, the algorithm that generates these certificates can be shown to be expected polynomial time for all but a small fraction of primes, and this fraction exponentially decreases with the size of the primes. Consequently, it's well-suited to generating certified large random primes, an application that is important in cryptography
applications such as generating provably valid RSA keys.
, a prime number could itself be considered a certificate of its own primality. This test runs in Õ((log n)6) time. In practice this method of verification is more expensive than the verification of Pratt certificates, but does not require any computation to determine the certificate itself.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a primality certificate or primality proof is a succinct, formal proof that a number is prime. Primality certificates allow the primality of a number to be rapidly checked without having to run an expensive or unreliable primality test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
. By "succinct", we usually mean that we wish for the proof to be at most polynomially larger than the number of digits in the number itself (for example, if the number has b bits, the proof might contain roughly b2 bits).
Primality certificates lead directly to proofs that problems such as primality testing and the complement
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
of integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
lie in NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, the class of problems verifiable in polynomial time given a solution. These problems already trivially lie in co-NP. This was the first strong evidence that these problems are not NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, since if they were it would imply NP = co-NP, a result widely believed to be false; in fact, this was the first demonstration of a problem in NP intersect co-NP not known (at the time) to be in P.
Producing certificates for the complement problem, to establish that a number is composite, is straightforward; it suffices to give a nontrivial divisor. Standard probabilistic primality tests such as the Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
and the Miller-Rabin primality test
Miller-Rabin primality test
The Miller–Rabin primality test or Rabin–Miller primality test is a primality test: an algorithmwhich determines whether a given number is prime,...
also produce compositeness certificates in the event where the input is composite, but do not produce certificates for prime inputs.
Pratt certificates
The concept of primality certificates was historically introduced by the Pratt certificate, conceived in 1975 by Vaughan Pratt, who described its structure and proved it to have polynomial size and to be verifiable in polynomial time. It is based on the Lucas primality test, which is essentially the converse of Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
with an added condition to make it true:
- Suppose we have an integer a such that:
- a is coprime to n;
- an −1 ≡ 1 (mod n)
- For every prime factor q of n −1, it is not the case that a(n −1)/q ≡ 1 (mod n).
- Then, n is prime.
Given such an a (called a witness) and the prime factorization of n−1, it's simple to verify the above conditions quickly: we only need to do a linear number of modular exponentiations, since every integer has fewer prime factors than bits, and each of these can be done by exponentiation by squaring
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
in O(log n) multiplications (see big-O notation). Even with grade-school integer multiplication, this is only O((log n)4) time; using the multiplication algorithm
Multiplication algorithm
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
with best-known asymptotic running time, the Schönhage–Strassen algorithm, we can lower this to O((log n)3(log log n)(log log log n)) time, or using soft-O notation Õ((log n)3).
However, it is possible to trick a verifier into accepting a composite number by giving it a "prime factorization" of n−1 that includes composite numbers. For example, suppose we claim that n=85 is prime, supplying a=4 and n−1=6×14 as the "prime factorization". Then (using q=6 and q=14):
- 4 is coprime to 85
- 485−1 ≡ 1 (mod 85)
- 4(85−1)/6 ≡ 16 (mod 85), 4(85−1)/14 ≡ 16 (mod 85)
We would falsely conclude that 85 is prime. We don't want to just force the verifier to factor the number, because there is no known general polynomial-time factoring algorithm.
A better way to avoid this issue is to give primality certificates for each of the prime factors of n−1 as well, which are just smaller instances of the original problem. We continue recursively in this manner until we reach a number known to be prime, such as 2. We end up with a tree of prime numbers, each associated with a witness a. For example, here is a complete Pratt certificate for the number 229:
- 229 (a=6, 229−1 = 22×3×19)
- 2 (known prime)
- 3 (a=2, 3−1 = 2)
- 2 (known prime)
- 19 (a=2, 19−1 = 2×32)
- 2 (known prime)
- 3 (a=2, 3−1 = 2)
- 2 (known prime)
This proof tree can be shown to contain at most
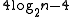 values other than 2 by a simple inductive proof (based on Theorem 2 of Pratt). The result holds for 3; in general, take p > 3 and let its children in the tree be p1,...,pk. By the inductive hypothesis the tree rooted at pi contains at most
values other than 2 by a simple inductive proof (based on Theorem 2 of Pratt). The result holds for 3; in general, take p > 3 and let its children in the tree be p1,...,pk. By the inductive hypothesis the tree rooted at pi contains at most 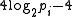 values, so the entire tree contains at most:
values, so the entire tree contains at most: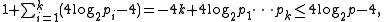
since k ≥ 2 and p1...pk = p−1. Since each value has at most log n bits, this also demonstrates that the certificate has a size of O((log n)2) bits.
Since there are O(log n) values other than 2 and each requires at most one exponentiation to verify (and exponentiations dominate the running time), the total time is O((log n)3(log log n)(log log log n)) or Õ((log n)3), which is quite feasible for numbers in the range that computational number theorists usually work with.
However, while useful in theory and easy to verify, actually generating a Pratt certificate for n requires factoring n−1 and other potentially large numbers. This is simple for some special numbers such as Fermat primes, but currently much more difficult than simple primality testing for large primes of general form.
Atkin–Goldwasser–Kilian–Morain certificates
To address the problem of efficient certificate generation for larger numbers, in 1986 Shafi GoldwasserShafi Goldwasser
Shafrira Goldwasser is the RSA Professor of electrical engineering and computer science at MIT, and a professor of mathematical sciences at the Weizmann Institute of Science, Israel.-Biography:...
and Joe Kilian described a new type of certificate based on the theory of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s. This was in turn used by A. O. L. Atkin
A. O. L. Atkin
Arthur Oliver Lonsdale Atkin , who published under the name A. O. L. Atkin, was a Professor Emeritus of mathematics at the University of Illinois at Chicago. As an undergraduate during World War II, he worked at Bletchley Park cracking German codes. He received his Ph.D...
and François Morain as the basis for Atkin-Goldwasser-Kilian-Morain certificates, which are the type of certificates generated and verified by elliptic curve primality proving
Elliptic curve primality proving
Elliptic Curve Primality Proving is a method based on elliptic curves to prove the primality of a number . It is a general-purpose algorithm, meaning it does not depend on the number being of a special form...
systems. Just as Pratt certificates are based on Lehmer's theorem, Atkin-Goldwasser-Kilian-Morain certificates are based on the following theorem of Goldwasser and Kilian (Lemma 2 of "Almost All Primes Can Be Quickly Certified"):
- Theorem: Suppose we are given:
- a positive integer n not divisible by 2 or 3;
- Mx,My,A,B in
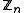 (the integers mod n) satisfying My2 = Mx3 + AMx + B and with 4A3 + 27B2 coprime to n;
(the integers mod n) satisfying My2 = Mx3 + AMx + B and with 4A3 + 27B2 coprime to n; - a prime
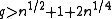 .
.
- Then M=(Mx,My) is a non-identity point on the elliptic curve y2 = x3 + Ax + B. Let kM be M added to itself k times using standard elliptic curve addition. Then, if qM is the identity element I, then n is prime.
Technically, an elliptic curve can only be constructed over a field, and
 is only a field if n is prime, so we seem to be assuming the result we're trying to prove. The difficulty arises in the elliptic curve addition algorithm, which takes inverses in the field that may not exist in
is only a field if n is prime, so we seem to be assuming the result we're trying to prove. The difficulty arises in the elliptic curve addition algorithm, which takes inverses in the field that may not exist in 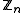 . However, it can be shown (Lemma 1 of "Almost All Primes Can Be Quickly Certified") that if we merely perform computations as though the curve were well-defined and do not at any point attempt to invert an element with no inverse, the result is still valid; if we do encounter an element with no inverse, this establishes that n is composite.
. However, it can be shown (Lemma 1 of "Almost All Primes Can Be Quickly Certified") that if we merely perform computations as though the curve were well-defined and do not at any point attempt to invert an element with no inverse, the result is still valid; if we do encounter an element with no inverse, this establishes that n is composite.To derive a certificate from this theorem, we first encode Mx, My, A, B, and q, then recursively encode the proof of primality for q < n, continuing until we reach a known prime. This certificate has size O((log n)2) and can be verified in O((log n)4) time. Moreover, the algorithm that generates these certificates can be shown to be expected polynomial time for all but a small fraction of primes, and this fraction exponentially decreases with the size of the primes. Consequently, it's well-suited to generating certified large random primes, an application that is important in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
applications such as generating provably valid RSA keys.
Impact of primes in P
Because primality testing can now be done deterministically in polynomial time using the AKS primality testAKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
, a prime number could itself be considered a certificate of its own primality. This test runs in Õ((log n)6) time. In practice this method of verification is more expensive than the verification of Pratt certificates, but does not require any computation to determine the certificate itself.
External links
- Mathworld: Primality Certificate
- Mathworld: Pratt Certificate
- Mathworld: Atkin-Goldwasser-Kilian-Morain Certificate
- Vašek Chvátal. Lecture notes on Pratt's Primality Proofs. Department of Computer Science. Rutgers University. PDF version at Concordia University.
- Wim van Dam. Proof of Pratt's Theorem. (Lecture notes, PDF)

