
Pre-measure
Encyclopedia
In mathematics
, a pre-measure is a function
that is, in some sense, a precursor to a bona fide
measure
on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory
, where they can be used to define measures such as Hausdorff measure
and packing measure on (subset
s of) metric space
s.
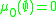
and, for every countable sequence
{An}n∈N ⊆ R of pairwise disjoint sets whose union lies in R,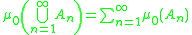 .
.
The second property is called σ-additivity
.
s, which are defined for all subsets of the space X. More precisely, if μ0 is a pre-measure defined on a ring of subsets R of the space X, then the set function μ∗ defined by

is an outer measure on X.
(Note that there is some variation in the terminology used in the literature. For example, Rogers (1998) uses "measure" where this article uses the term "outer measure". Outer measures are not, in general, measures, since they may fail to be σ-additive.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pre-measure is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is, in some sense, a precursor to a bona fide
Bona Fide
Bona Fide is a studio album from rock band Wishbone Ash. It is the first studio album in six years and is the only studio album to feature guitarist Ben Granfelt...
measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory
Dimension theory
In mathematics, dimension theory is a branch of general topology dealing with dimensional invariants of topological spaces.-See also:*Lebesgue covering dimension*Inductive dimensions *Dimension...
, where they can be used to define measures such as Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
and packing measure on (subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of) metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s.
Definition
Let R be a ring of subsets of a fixed set X and let μ0: R → [0, +∞] be a set function. μ0 is called a pre-measure if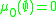
and, for every countable sequence
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
{An}n∈N ⊆ R of pairwise disjoint sets whose union lies in R,
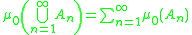 .
.The second property is called σ-additivity
Sigma additivity
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :...
.
Extension theorem
It turns out that pre-measures can be extended quite naturally to outer measureOuter measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
s, which are defined for all subsets of the space X. More precisely, if μ0 is a pre-measure defined on a ring of subsets R of the space X, then the set function μ∗ defined by

is an outer measure on X.
(Note that there is some variation in the terminology used in the literature. For example, Rogers (1998) uses "measure" where this article uses the term "outer measure". Outer measures are not, in general, measures, since they may fail to be σ-additive.)

