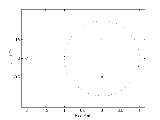
Pole-zero plot
Encyclopedia
In mathematics
, signal processing
and control theory
, a pole–zero plot is a graphical representation of a rational
transfer function
in the complex plane which helps to convey certain properties of the system such as:
In general, a rational transfer function for a discrete LTI system
has the form:
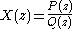
where
In the plot, the poles of the system are indicated by an x while the zeroes are indicated by an o.
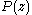 and
and  are completely factored, their solution can be easily plotted in the z-plane. For example, given the following transfer function:
are completely factored, their solution can be easily plotted in the z-plane. For example, given the following transfer function:
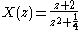
The only zero is located at: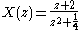 , and the two poles are located at:
, and the two poles are located at: 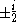 .
.
The pole–zero plot would be:
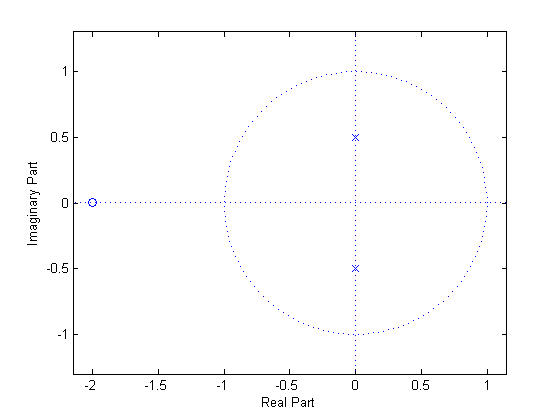
or annulus
which contains no poles.
The choice of ROC is not unique, however the ROC is usually chosen to include the unit circle since it is important for most practical systems to have Bounded Input, Bounded Output (BIBO) stability
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, a pole–zero plot is a graphical representation of a rational
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
in the complex plane which helps to convey certain properties of the system such as:
- StabilityBIBO stabilityIn electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
- Causal systemCausal systemA causal system is a system where the output depends on past/current inputs but not future inputs i.e...
/ anticausal systemAnticausal systemAn anticausal system is a hypothetical system with outputs and internal states that depend solely on future input values. Some textbooks and published research literature might define an anticausal system to be one that does not depend on past input values An anticausal system is a hypothetical... - Region of convergence (ROC)Radius of convergenceIn mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
- Minimum phaseMinimum phaseIn control theory and signal processing, a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable....
/ non minimum phase
In general, a rational transfer function for a discrete LTI system
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
has the form:
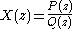
where
-
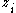 such that
such that 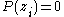 are the zeroZero (complex analysis)In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
are the zeroZero (complex analysis)In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
s of the system -
 such that
such that 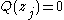 are the poles of the system
are the poles of the system
In the plot, the poles of the system are indicated by an x while the zeroes are indicated by an o.
Example
If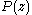 and
and  are completely factored, their solution can be easily plotted in the z-plane. For example, given the following transfer function:
are completely factored, their solution can be easily plotted in the z-plane. For example, given the following transfer function: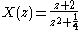
The only zero is located at:
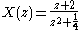 , and the two poles are located at:
, and the two poles are located at: 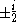 .
.The pole–zero plot would be:

Interpretation
The region of convergence (ROC) for a given transfer function is a diskDisk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
or annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
which contains no poles.
- If the disc includes the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, then the system is BIBO stableBIBO stabilityIn electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
. - If the region of convergence extends outward from the largest pole (not at infinity), then the system is right-sided.
- If the region of convergence extends inward from the smallest nonzero pole, then the system is left-sided.
The choice of ROC is not unique, however the ROC is usually chosen to include the unit circle since it is important for most practical systems to have Bounded Input, Bounded Output (BIBO) stability
BIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
.

