
Plücker embedding
Encyclopedia
In mathematics, the Plücker embedding describes a method to realize the Grassmannian
of all r-dimensional subspaces of a vector space
V as a subvariety of the projective space of the rth exterior power of that vector space, P(∧r V).
The Plücker embedding was first defined, in the case r = 2, n = 4, in coordinates
by Julius Plücker
as a way of describing the lines in three dimensional space (which, as projective line
s in real projective space
, correspond to two dimensional subspaces of a four dimensional vector space). This was generalized by Hermann Grassmann
to arbitrary r and n using a generalization of Plücker's coordinates, sometimes called Grassmann coordinates.
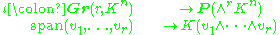
where Gr(r, Kn) is the Grassmannian
, i.e., the space of all r-dimensional subspaces of the n-dimensional vector space
, Kn.
This is an isomorphism from the Grassmannian to the image of ι, which is a projective variety. This variety can be completely characterized as an intersection of quadrics, each coming from a relation on the Plücker (or Grassmann) coordinates that derives from linear algebra.
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of all r-dimensional subspaces of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V as a subvariety of the projective space of the rth exterior power of that vector space, P(∧r V).
The Plücker embedding was first defined, in the case r = 2, n = 4, in coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
by Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
as a way of describing the lines in three dimensional space (which, as projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
s in real projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, correspond to two dimensional subspaces of a four dimensional vector space). This was generalized by Hermann Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
to arbitrary r and n using a generalization of Plücker's coordinates, sometimes called Grassmann coordinates.
Definition
The Plücker embedding (over the field K) is the map ι defined by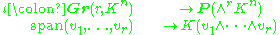
where Gr(r, Kn) is the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
, i.e., the space of all r-dimensional subspaces of the n-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, Kn.
This is an isomorphism from the Grassmannian to the image of ι, which is a projective variety. This variety can be completely characterized as an intersection of quadrics, each coming from a relation on the Plücker (or Grassmann) coordinates that derives from linear algebra.

