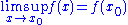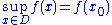Plurisubharmonic function
Encyclopedia
In mathematics
, plurisubharmonic functions (sometimes abbreviated as psh, plsh, or plush functions) form an important class of functions
used in complex analysis
. On a Kähler manifold
, plurisubharmonic functions form a subset of the subharmonic function
s. However, unlike subharmonic functions (which are defined on a Riemannian manifold
) plurisubharmonic functions can be defined in full generality on complex space
s.
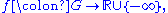
with domain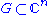
is called plurisubharmonic if it is upper semi-continuous, and for every complex
line
 with
with 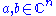
the function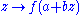 is a subharmonic function
is a subharmonic function
on the set
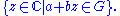
In full generality, the notion can be defined on an arbitrary complex manifold
or even a complex space
 as follows. An upper semi-continuous function
as follows. An upper semi-continuous function
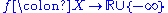
is said to be plurisubharmonic if and only if for any holomorphic map
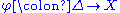 the function
the function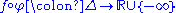
is subharmonic
, where denotes the unit disk.
denotes the unit disk.
 is of (differentiability) class
is of (differentiability) class 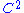 , then
, then  is plurisubharmonic, if and only if the hermitian matrix
is plurisubharmonic, if and only if the hermitian matrix 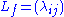 , called Levi matrix, with
, called Levi matrix, with
entries
is positive semidefinite.
Equivalently, a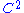 -function f is plurisubharmonic if and only if
-function f is plurisubharmonic if and only if 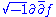 is a positive (1,1)-form
is a positive (1,1)-form
.
Kiyoshi Oka
and Pierre Lelong.
then so is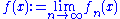 .
.
(see limit superior and limit inferior
for the definition of lim sup).
for some point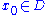 then
then 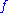 is constant.
is constant.
, plurisubharmonic functions are used to describe pseudoconvex domains, domains of holomorphy
and Stein manifold
s.
in 1942.
A continuous function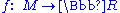
is called exhaustive if the preimage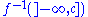
is compact for all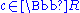 . A plurisubharmonic
. A plurisubharmonic
function f is called strongly plurisubharmonic
if the form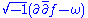
is positive
, for some Kähler form
 on M.
on M.
Theorem of Oka: Let M be a complex manifold,
admitting a smooth, exhaustive, strongly plurisubharmonic function.
Then M is Stein
. Conversely, any
Stein manifold
admits such a function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, plurisubharmonic functions (sometimes abbreviated as psh, plsh, or plush functions) form an important class of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
used in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. On a Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, plurisubharmonic functions form a subset of the subharmonic function
Subharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
s. However, unlike subharmonic functions (which are defined on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
) plurisubharmonic functions can be defined in full generality on complex space
Complex space
In mathematics, n-dimensional complex space is a multi-dimensional generalisation of the complex numbers, which have both real and imaginary parts or dimensions...
s.
Formal definition
A functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
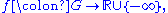
with domain
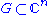
is called plurisubharmonic if it is upper semi-continuous, and for every complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
line
 with
with 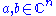
the function
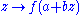 is a subharmonic function
is a subharmonic functionSubharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
on the set
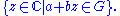
In full generality, the notion can be defined on an arbitrary complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
or even a complex space
Complex space
In mathematics, n-dimensional complex space is a multi-dimensional generalisation of the complex numbers, which have both real and imaginary parts or dimensions...
 as follows. An upper semi-continuous function
as follows. An upper semi-continuous functionSemi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
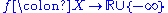
is said to be plurisubharmonic if and only if for any holomorphic map
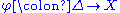 the function
the function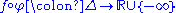
is subharmonic
Subharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
, where
 denotes the unit disk.
denotes the unit disk.Differentiable plurisubharmonic functions
If is of (differentiability) class
is of (differentiability) class 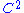 , then
, then  is plurisubharmonic, if and only if the hermitian matrix
is plurisubharmonic, if and only if the hermitian matrix 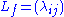 , called Levi matrix, with
, called Levi matrix, withentries
is positive semidefinite.
Equivalently, a
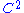 -function f is plurisubharmonic if and only if
-function f is plurisubharmonic if and only if 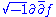 is a positive (1,1)-form
is a positive (1,1)-formPositive form
In complex geometry, the term positive formrefers to several classes of real differential formsof Hodge type .- -forms :Real -forms on a complex manifold Mare forms which are of type and real,...
.
History
Plurisubharmonic functions were defined in 1942 byKiyoshi Oka
Kiyoshi Oka
was a Japanese mathematician who did fundamental work in the theory of several complex variables. He was born in Osaka. He went to Kyoto Imperial University in 1919, turning to mathematics in 1923 and graduating in 1924....
and Pierre Lelong.
Properties
- The set of plurisubharmonic functions form a convex coneConvex coneIn linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
in the vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of semicontinuous functions, i.e. - if
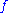 is a plurisubharmonic function and
is a plurisubharmonic function and  a positive real number, then the function
a positive real number, then the function 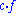 is plurisubharmonic,
is plurisubharmonic, - if
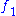 and
and 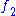 are plurisubharmonic functions, then the sum
are plurisubharmonic functions, then the sum 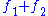 is a plurisubharmonic function.
is a plurisubharmonic function. - Plurisubharmonicity is a local property, i.e. a function is plurisubharmonic if and only if it is plurisubharmonic in a neighborhood of each point.
- If
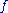 is plurisubharmonic and
is plurisubharmonic and 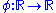 a monotonically increasing, convex function then
a monotonically increasing, convex function then 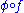 is plurisubharmonic.
is plurisubharmonic. - If
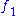 and
and 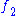 are plurisubharmonic functions, then the function
are plurisubharmonic functions, then the function 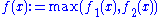 is plurisubharmonic.
is plurisubharmonic. - If
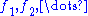 is a monotonically decreasing sequence of plurisubharmonic functions
is a monotonically decreasing sequence of plurisubharmonic functions
then so is
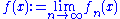 .
.
- Every continuous plurisubharmonic function can be obtained as a limit of monotonically decreasing sequence of smooth plurisubharmonic functions. Moreover, this sequence can be chosen uniformly convergent.
- The inequality in the usual semi-continuitySemi-continuityIn mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
condition holds as equality, i.e. if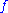 is plurisubharmonic then
is plurisubharmonic then
(see limit superior and limit inferior
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
for the definition of lim sup).
- Plurisubharmonic functions are subharmonicSubharmonic functionIn mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
, for any Kähler metricKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
.
- Therefore, plurisubharmonic functions satisfy the maximum principleMaximum principleIn mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
, i.e. if is plurisubharmonic on the connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
is plurisubharmonic on the connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
domain and
and
for some point
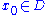 then
then 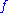 is constant.
is constant.Applications
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, plurisubharmonic functions are used to describe pseudoconvex domains, domains of holomorphy
Domain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
and Stein manifold
Stein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
s.
Oka theorem
The main geometric application of the theory of plurisubharmonic functions is the famous theorem proven by Kiyoshi OkaKiyoshi Oka
was a Japanese mathematician who did fundamental work in the theory of several complex variables. He was born in Osaka. He went to Kyoto Imperial University in 1919, turning to mathematics in 1923 and graduating in 1924....
in 1942.
A continuous function
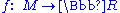
is called exhaustive if the preimage
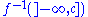
is compact for all
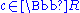 . A plurisubharmonic
. A plurisubharmonicfunction f is called strongly plurisubharmonic
if the form
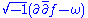
is positive
Positive form
In complex geometry, the term positive formrefers to several classes of real differential formsof Hodge type .- -forms :Real -forms on a complex manifold Mare forms which are of type and real,...
, for some Kähler form
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
 on M.
on M.Theorem of Oka: Let M be a complex manifold,
admitting a smooth, exhaustive, strongly plurisubharmonic function.
Then M is Stein
Stein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
. Conversely, any
Stein manifold
Stein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
admits such a function.