Playfair's axiom is a geometrical axiom

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

, intended to replace the fifth postulate of Euclides (the Parallel postulate

Parallel postulate

In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...

):

Given a line and a point not on it, at most one parallel

Parallel (geometry)

Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...

 to the given line can be drawn through the point.

It is equivalent to Euclid's parallel postulate

Parallel postulate

In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...

 and was named after the Scottish mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 John Playfair

John Playfair

John Playfair FRSE, FRS was a Scottish scientist and mathematician, and a professor of natural philosophy at the University of Edinburgh. He is perhaps best known for his book Illustrations of the Huttonian Theory of the Earth , which summarized the work of James Hutton...

. It is only required to state "at most" because the rest of the postulates will imply that there is exactly one. It could perfectly be assumed to write it saying "there is one and only one parallel".

It is important to remark that in the Euclid book, two lines are said to be parallel if they never meet. It does not matter if their distance is always the same or not.

When David Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

 made his Hilbert's axioms

Hilbert's axioms

Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie , as the foundation for a modern treatment of Euclidean geometry...

 he used Playfair's axiom instead of the original one from Euclid.

History

In 1795 Playfair published an alternative, more stringent formulation of Euclid's parallel postulate, which is now called Playfair's axiom; though the axiom bears Playfair's name, he did not create it, but credited others, in particular William Ludlam (1718–1788), with the prior use of it.

Relation with Euclid's fifth postulate

Playfair's axiom is not exactly equivalent to Euclid's Fifth Postulate because on an elliptical geometry, such as the surface of a sphere, Euclid's postulate in its original version:

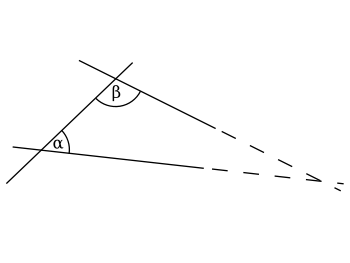
If a line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

 intersects two straight lines

Line (mathematics)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

 forming two interior angles on the same side that sum to less than two right angle

Right angle

In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

s, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

holds because two lines on a sphere always meet. Playfair's postulate is therefore stronger and prevents elliptic geometries. Therefore, it is not possible to derive Playfair's postulate from Euclid Fifth alone.

Euclid's fifth postulate with the other four implies Playfair's postulate

The easiest way to show this is using the Euclid theorem (based in the fifth postulate) that states that the angles of a triangle are two right angles. Given a line and a point, construct a line perpendicular to the given one by the point, and a perpendicular to the perpendicular. This line is parallel because it cannot form a triangle. Now it can be seen that no more parallels exist because any line that forms an angle with the second one will cut the first one.

Playfair's implies Euclid's fifth postulate

Given that Playfair's postulate implies that only the perpendicular to the perpendicular is a parallel, the lines of the Euclid construction will have to cut each other in a point. It is also necessary to prove that they will do it in the side where the angles are less than two right angles, but this is more difficult.