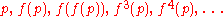Periodic sequence
Encyclopedia
In mathematics
, a periodic sequence is a sequence
for which the same terms are repeated over and over:
The number p of repeated terms is called the period.
for all values of n. If we regard a sequence as a function
whose domain is the set of natural number
s, then a periodic sequence is simply a special type of periodic function
.
expansion of 1/7 is periodic with period six:
More generally, the sequence of digits in the decimal expansion of any rational number
is eventually periodic (see below).
The sequence of powers of −1 is periodic with period two:
More generally, the sequence of powers of any root of unity
is periodic. The same holds true for the powers of any element of finite order
in a group
.
A periodic point
for a function ƒ: X → X is a point p whose orbit
is a periodic sequence. Periodic points are important in the theory of dynamical systems.
A sequence is asymptotically periodic if its terms approach those of a periodic sequence. That is, the sequence x1, x2, x3, ... is asymptotically periodic if there exists a periodic sequence a1, a2, a3, ... for which
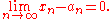
For example, the sequence
is asymptotically periodic, since its terms approach those of the periodic sequence 0, 1, 0, 1, 0, 1, ....
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a periodic sequence is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
for which the same terms are repeated over and over:
- a1, a2, ..., ap, a1, a2, ..., ap, a1, a2, ..., ap, ...
The number p of repeated terms is called the period.
Definition
A periodic sequence is a sequence a1, a2, a3, ... satisfying- an+p = an
for all values of n. If we regard a sequence as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
whose domain is the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, then a periodic sequence is simply a special type of periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
.
Examples
The sequence of digits in the decimalDecimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
expansion of 1/7 is periodic with period six:
- 1 / 7 = 0 . 1 4 2 8 5 7 1 4 2 8 5 7 1 4 2 8 5 7 ...
More generally, the sequence of digits in the decimal expansion of any rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
is eventually periodic (see below).
The sequence of powers of −1 is periodic with period two:
- −1, +1, −1, +1, −1, +1, ...
More generally, the sequence of powers of any root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
is periodic. The same holds true for the powers of any element of finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
in a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
A periodic point
Periodic point
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
for a function ƒ: X → X is a point p whose orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
is a periodic sequence. Periodic points are important in the theory of dynamical systems.
Generalizations
A sequence is eventually periodic if it can be made periodic by dropping some finite number of terms from the beginning. For example, the sequence of digits in the decimal expansion of 1/56 is eventually periodic:- 1 / 56 = 0 . 0 1 7 8 5 7 1 4 2 8 5 7 1 4 2 8 5 7 1 4 2 ...
A sequence is asymptotically periodic if its terms approach those of a periodic sequence. That is, the sequence x1, x2, x3, ... is asymptotically periodic if there exists a periodic sequence a1, a2, a3, ... for which
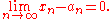
For example, the sequence
- 1 / 3, 2 / 3, 1 / 4, 3 / 4, 1 / 5, 4 / 5, ...
is asymptotically periodic, since its terms approach those of the periodic sequence 0, 1, 0, 1, 0, 1, ....