Percentage
Encyclopedia
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a percentage is a way of expressing a number as a fraction
Fraction
In common usage a fraction is any part of a unit.Fraction may also mean:*Fraction , one of more equal parts of something, eg...
of 100 (per centum meaning “per hundred” in Latin). It is often denoted using the percent sign
Percent sign
The percent sign is the symbol used to indicate a percentage .Related signs include the permille sign ‰ and the permyriad sign , which indicate that a number is divided by one thousand or ten thousand respectively...
, “%”, or the abbreviation “pct”. For example, 45% (read as “forty-five percent”) is equal to 45/100
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, or 0.45.
Percentages are used to express how large/small one quantity is, relative to another quantity. The first quantity usually represents a part of, or a change in, the second quantity, which should be greater than zero. For example, an increase of $ 0.15 on a price of $ 2.50 is an increase by a fraction of 0.15/2.50 = 0.06. Expressed as a percentage, this is therefore a 6% increase.
Although percentages are usually used to express numbers between zero and one, any dimensionless proportionality
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
can be expressed as a percentage. For instance, 111% is 1.11 and −0.35% is −0.0035. Although this is technically inaccurate as per the definition of percent, an alternative wording in terms of a change in an observed value is “an increase/decrease by a factor of...””
Calculations
The fundamental concept to remember when performing calculations with percentages is that the percent symbol can be treated as being equivalent to the pure number constant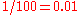
, for example 35% of 300 can be written as .To find the percentage that a single unit represents out of a whole of N units, divide 100% by N. For instance, if you have 1250 apples, and you want to find out what percentage of these 1250 apples a single apple represents, provides the answer of 0.08%. So, if you give away one apple, you have given away 0.08% of the apples you had. Then, if instead you give away 100 apples, you have given away 100 × 0.08% = 8% of your 1250 apples.
To calculate a percentage of a percentage, convert both percentages to fractions of 100, or to decimals, and multiply them. For example, 50% of 40% is:
It is not correct to divide by 100 and use the percent sign at the same time. (E.g. , not , which actually is .)
The easy way to calculate addition in percentage (discount 10% + 5%):
- y = [(x1+x2) - (x1*x2)/100%]
For example, in a department store promotion "discount 10%+5%", the total discount is not 15%, but:
-
Example problems
Whenever we talk about a percentage, it is important to specify what it is relative to, i.e. what is the total that corresponds to 100%. The following problem illustrates this point.
- In a certain college 60% of all students are female, and 10% of all students are computer science majors. If 5% of female students are computer science majors, what percentage of computer science majors are female?
We are asked to compute the ratioRatioIn mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of female computer science majors to all computer science majors. We know that 60% of all students are female, and among these 5% are computer science majors, so we conclude that (60/100) × (5/100) = 3/100 or 3% of all students are female computer science majors. Dividing this by the 10% of all students that are computer science majors, we arrive at the answer: 3%/10% = 30/100 or 30% of all computer science majors are female.
This example is closely related to the concept of conditional probabilityConditional probabilityIn probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
.
Here are other examples:
- What is
of 
?
- Answer:
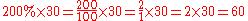
- Answer:
- What is
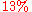of 
?
- Answer:
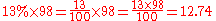
- Answer:
-
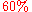of all university students are female. There are 
female students. How many students are in the university?
- Answer:
, therefore 
.
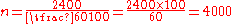- Answer:
- There are
cats in the village, and 
of them are black. What is the percentage of black cats in that village?
- Answer:
, so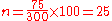 
and therefore 
.
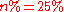- Answer:
- The number of students at the university increased to
, compared to last year's 
, an absolute increase of 
students. What is the percentual increase?
- Answer:
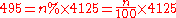, so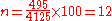 
, and therefore 
.
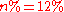- Answer:
Percentage increase and decrease
Sometimes due to inconsistent usage, it is not always clear from the context what a percentage is relative to. When speaking of a "10% rise" or a "10% fall" in a quantity, the usual interpretation is that this is relative to the initial value of that quantity. For example, if an item is initially priced at $200 and the price rises 10% (an increase of $20), the new price will be $220. Note that this final price is 110% of the initial price (100% + 10% = 110%).
Some other examples of percent changes:- An increase of 100% in a quantity means that the final amount is 200% of the initial amount (100% of initial + 100% of increase = 200% of initial); in other words, the quantity has doubled.
- An increase of 800% means the final amount is 9 times the original (100% + 800% = 900% = 9 times as large).
- A decrease of 60% means the final amount is 40% of the original (100% − 60% = 40%).
- A decrease of 100% means the final amount is zero (100% − 100% = 0%).
In general, a change of
percent in a quantity results in a final amount that is 
percent of the original amount (equivalently,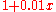 
times the original amount).
It is important to understand that percent changes, as they have been discussed here, do not add in the usual way, if applied sequentially. For example, if the 10% increase in price considered earlier (on the $200 item, raising its price to $220) is followed by a 10% decrease in the price (a decrease of $22), the final price will be $198, not the original price of $200. The reason for the apparent discrepancy is that the two percent changes (+10% and −10%) are measured relative to different quantities ($200 and $220, respectively), and thus do not "cancel out".
Another common mistake is thinking that working 50% faster means taking 50% less time to complete the task. On this account, 100% faster means twice the speed, so half the time. For example, if one traveled at 50 mph, 100% faster would be 100 mph (taking 50% less time). And 50% faster speed means 33.33% less time to travel the same distance.
In general, if an increase of
percent is followed by a decrease of 
percent, and the initial amount was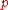 
, the final amount is 
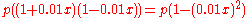; thus the net change is an overall decrease by 
percent of 
percent (the square of the original percent change when expressed as a decimal number). Thus, in the above example, after an increase and decrease of 
percent, the final amount, $198, was 10% of 10%, or 1%, less than the initial amount of $200.
This can be expanded for a case where you do not have the same percent change. If the initial percent change is
and the second percent change is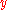 
, and the initial amount was 
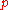, then the final amount is 
. To change the above example, after an increase of 
and decrease of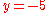 
percent, the final amount, $209, is 4.5% more than the initial amount of $200.
In the case of interest rateInterest rateAn interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
s, it is a common practice to state the percent change differently. If an interest rate rises from 10% to 15%, for example, it is typical to say, "The interest rate increased by 5%" — rather than by 50%, which would be correct when measured as a percentage of the initial rate (i.e., from 0.10 to 0.15 is an increase of 50%). Such ambiguity can be avoided by using the term "percentage pointPercentage pointPercentage points are the unit for the arithmetic difference of two percentages.Consider the following hypothetical example: in 1980, 40 percent of the population smoked, and in 1990 only 30 percent smoked...
s". In the previous example, the interest rate "increased by 5 percentage points" from 10% to 15%. If the rate then drops by 5 percentage points, it will return to the initial rate of 10%, as expected.
Change in sign
When the first number is negative and second number is positive, the percentage change from first number to second number is negative.
This often occurs in financial statements that changes from a period of loss to period in profit.
Acme Company EBIT
First quarter (100)
Second quarter 100
Change in profitability (100 - (-100))/(-100) = -200%
In expressing a number as a percentage, the base of the comparison cannot be negative.
The First number in the above example is the base of the comparison when it is expressed as a positive amount becomes Loss of 100.
The change from First quarter loss to Second quarter profit becomes Percentage change in loss by -200% to turn a profit of 100.
Word and symbol
In British EnglishBritish EnglishBritish English, or English , is the broad term used to distinguish the forms of the English language used in the United Kingdom from forms used elsewhere...
, percent is usually written as two words (per cent, although percentage and percentile are written as one word). In American EnglishAmerican EnglishAmerican English is a set of dialects of the English language used mostly in the United States. Approximately two-thirds of the world's native speakers of English live in the United States....
, percent is the most common variant (but cf. per mille written as two words).
In the early part of the twentieth century, there was a dotted abbreviation form “per cent.”, as opposed to “per cent”. The form “per cent.” is still in use as a part of the highly formal language found in certain documents like commercial loan agreements (particularly those subject to, or inspired by, common law), as well as in the HansardHansardHansard is the name of the printed transcripts of parliamentary debates in the Westminster system of government. It is named after Thomas Curson Hansard, an early printer and publisher of these transcripts.-Origins:...
transcripts of British Parliamentary proceedings. While the term has been attributed to LatinLatinLatin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
per centum, this is a pseudo-LatinDog LatinDog Latin, Cod Latin, macaronic Latin, or mock Latin refers to the creation of a phrase or jargon in imitation of Latin, often by directly translating English words into Latin without conjugation or declension...
construction and the term was likely originally adopted from the FrenchFrench languageFrench is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
pour cent. The concept of considering values as parts of a hundred is originally GreekAncient GreeceAncient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
. The symbol for percentPercent signThe percent sign is the symbol used to indicate a percentage .Related signs include the permille sign ‰ and the permyriad sign , which indicate that a number is divided by one thousand or ten thousand respectively...
(%) evolved from a symbol abbreviating the Italian per cento. In some other languages, the form prosent is used instead. Some languages use both a word derived from percent and an expression in that language meaning the same thing, e.g. Romanian procent and la sută (thus, 10 % can be read or sometimes written ten for [each] hundred, similarly with the English one out of ten). Other abbreviations are rarer, but sometimes seen.
Grammar and style guides often differ as to how percentages are to be written. For instance, it is commonly suggested that the word percent (or per cent) be spelled out in all texts, as in “1 percent” and not “1%”. Other guides prefer the word to be written out in humanistic texts, but the symbol to be used in scientific texts. Most guides agree that they always be written with a numeral, as in “5 percent” and not “five percent”, the only exception being at the beginning of a sentence: “Ten percent of all writers love style guides.” Decimals are also to be used instead of fractions, as in “3.5 percent of the gain” and not “3 ½ percent of the gain”. It is also widely accepted to use the percent symbol (%) in tabular and graphic material.
In line with common English practice, style guides—such as the The Chicago Manual of StyleThe Chicago Manual of StyleThe Chicago Manual of Style is a style guide for American English published since 1906 by the University of Chicago Press. Its 16 editions have prescribed writing and citation styles widely used in publishing...
—generally state that the number and percent sign are written without any space in between.
However, the International System of UnitsInternational System of UnitsThe International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
and the ISO 31-0ISO 31-0ISO 31-0 is the introductory part of international standard ISO 31 on quantities and units. It provides guidelines for using physical quantities, quantity and unit symbols, and coherent unit systems, especially the SI...
standard require a space.
Related units
- Percentage pointPercentage pointPercentage points are the unit for the arithmetic difference of two percentages.Consider the following hypothetical example: in 1980, 40 percent of the population smoked, and in 1990 only 30 percent smoked...
- Per millePermilleA per mil or per mille is a tenth of a percent or one part per thousand. It is written with the sign ‰ , which looks like a percent sign with an extra zero at the end...
(‰) 1 part in 1,000 - Basis pointBasis pointA basis point is a unit equal to 1/100 of a percentage point or one part per ten thousand...
1 part in 10,000 - Per cent millePer cent milleA per cent mille or pcm is one one-thousandth of a percent. It can be thought of as a "milli-percent". It is commonly used in nuclear reactor engineering....
(pcm) 1 part in 100,000 - Parts-per notationParts-per notationIn science and engineering, the parts-per notation is a set of pseudo units to describe small values of miscellaneous dimensionless quantities, e.g. mole fraction or mass fraction. Since these fractions are quantity-per-quantity measures, they are pure numbers with no associated units of measurement...
- Baker percentageBaker percentageBaker's percentage is a baker's notation method indicating the flour-relative proportion of ingredients used when making breads, cakes, muffins, and other pastries. It is also referred to as baker's math, or otherwise contextually indicated by a phrase such as based on flour weight...
- ConcentrationConcentrationIn chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
- Grade (slope)
- Volume percent
- Per-unit systemPer-unit systemIn the power transmission field of electrical engineering, a per-unit system is the expression of system quantities as fractions of a defined base unit quantity. Calculations are simplified because quantities expressed as per-unit are the same regardless of the voltage level...
Other uses
It is well known that many in the media and sports worlds use clichés such as '110%' despite the fact that such phrases do not make any mathematical sense.
The word "percentage" is often misused in the context of sports statistics, when the referenced number is expressed as a decimal proportion, not a percentage: "The Phoenix Suns'Phoenix SunsThe Phoenix Suns are a professional basketball team based in Phoenix, Arizona. They are members of the Pacific Division of the Western Conference in the National Basketball Association and the only team in their division not to be based in California. Their home arena since 1992 has been the US...
Shaquille O'NealShaquille O'NealShaquille Rashaun O'Neal , nicknamed "Shaq" , is a former American professional basketball player. Standing tall and weighing , he was one of the heaviest players ever to play in the NBA...
led the NBA with a .609 field goal percentageField goal percentageField goal percentage in basketball is the ratio of field goals made to field goals attempted. Its abbreviation is FG%. Three-point field goals are included in this percentage. Instead of using scales of 0 to 100%, the scale .000 to 1.000 is commonly used. A higher field goal percentage denotes...
(FG%) during the 2008-09 season." (O'Neal made 60.9% of his shots, not 0.609%.) The practice is probably related to the similar way that batting averageBatting averageBatting average is a statistic in both cricket and baseball that measures the performance of cricket batsmen and baseball hitters. The two statistics are related in that baseball averages are directly descended from the concept of cricket averages.- Cricket :...
s are quoted.
As "percent" it is used to describe the steepness of the slope of a roadRoadA road is a thoroughfare, route, or way on land between two places, which typically has been paved or otherwise improved to allow travel by some conveyance, including a horse, cart, or motor vehicle. Roads consist of one, or sometimes two, roadways each with one or more lanes and also any...
or railwayRail tracksThe track on a railway or railroad, also known as the permanent way, is the structure consisting of the rails, fasteners, sleepers and ballast , plus the underlying subgrade...
.
External links
- Express learning - percentages BBC raw money