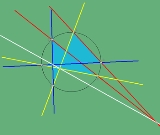
Pascal's theorem
Encyclopedia
In projective geometry
, Pascal's theorem (aka Hexagrammum Mysticum Theorem) states that if an arbitrary hexagon is inscribed in any conic section
, and pairs of opposite side
s are extended until they meet, the three intersection
points will lie on a straight line, the Pascal line of that configuration.
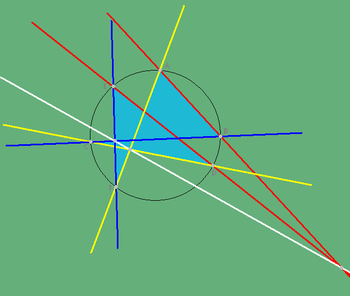
– Pappus's theorem is the special case of a degenerate conic
of two lines. Pascal's theorem is the polar reciprocal and projective dual of Brianchon's theorem
. It was discovered by Blaise Pascal
in 1639 when he was 16 years old.
A degenerate case of Pascal's Theorem is interesting indeed; given four points ABCD on a conic Γ, AB ∩ CD, BC ∩ DA, intersection of tangents at (A, C) and (B, D) are collinear (four points). This property can be proven independently using a property of pole-polar. If the conic is a circle, then another degenerate case tells us that for a triangle, the three points that appear as the intersection of a side line with the corresponding side line of the Gergonne triangle, are collinear, see Gergonne triangle.
Six is the minimum number of points on a conic about which special statements can be made, as five points determine a conic
.
The converse is the Braikenridge–Maclaurin theorem
, named for 18th century British mathematicians William Braikenridge and Colin Maclaurin
, which states that if the 3 intersection points of the lines through three sides of a hexagon lie on a line, then the 6 vertices of the hexagon lie on a conic; the conic may be degenerate, as in Pappus's theorem. The Braikenridge–Maclaurin theorem may be applied in the Braikenridge–Maclaurin construction, which is a synthetic
construction of the conic defined by five points, by varying the sixth point.
The theorem was generalized by Möbius
in 1847, as follows: suppose a polygon with 4n + 2 sides is inscribed in a conic section, and opposite pairs of sides are extended until they meet in 2n + 1 points. Then if 2n of those points lie on a common line, the last point will be on that line, too.
If six unordered points are given on a conic section, they can be connected into a hexagon in 60 different ways, resulting in 60 different instances of Pascal's theorem and 60 different Pascal lines.
As Thomas Kirkman proved in 1849, these 60 lines can be associated with 60 points in such a way that each point is on three lines and each line contains three points, forming a projective configuration. The 60 points formed in this way are now known as the Kirkman points .
It is sufficient to prove the theorem when the conic is a circle, because any (non-degenerate) conic can be reduced to a circle by a projective transformation; degenerate conics follow by continuity (the theorem is true for non-degenerate conics, and thus holds in the limit of degenerate conic).
A short elementary proof of Pascal's theorem in the case of a circle was found by , based on the proof in . This proof proves the theorem for circle and then generalizes it to conics.
We can infer the proof from existence of isogonal conjugate too. If we are to show that X = AB ∩ DE, Y = BC ∩ EF, Z = CD ∩ FA are collinear for conconical ABCDEF, then notice that ADY and CYF are similar, and that X and Z will correspond to the isogonal conjugate if we overlap the similar triangles. This means that angle DYX = angle CYZ, hence making XYZ collinear.
A short proof can be constructed using cross-ratio preservation. Projecting tetrad ABCE from D onto line AB, we obtain tetrad ABPX, and projecting tetrad ABCE from F onto line BC, we obtain tetrad QBCY. This therefore means that R(AB; PX) = R(QB; CY), where one of the points in the two tetrads overlap, hence meaning that other lines connecting the other three pairs must coincide to preserve cross ratio. Therefore XYZ are collinear.
Another proof for Pascal's theorem for a circle uses Menelaus' theorem
repeatedly.
Dandelin, the geometer who discovered the celebrated Dandelin spheres
, came up with a beautiful proof using "3D lifting" technique that is analogous to the 3D proof of Desargues' theorem
. The proof makes use of the property that for every conic section we can find a one-sheet hyperboloid which passes through the conic.
Also there exist a simple proof for Pascal's theorem for a circle uses Law of Sines
and similarity
.
The Cayley–Bacharach theorem is also used to prove that the group operation on cubic elliptic curves is associative. The same group operation can be applied on a cone if we choose a point E on the cone and a line MP in the plane. The sum of A and B is obtained by first finding the intersection point of line AB with MP, which is M. Next A and B add up to the second intersection point of the cone with line EM, which is D. Thus if Q is the second intersection point of the cone with line EN, then

Thus the group operation is associative. On the other hand, Pascal's theorem follows from the above associativity formula, and thus from the associativity of the group operation of elliptic curves by way of continuity.
a cubic and a conic have at most 3 × 2 = 6 points in common, unless they have a common component. So the cubic h = 0 has a component in common with the conic which must be the conic itself, so h = 0 is the union of the conic and a line. It is now easy to check that this line is the Pascal line.
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, Pascal's theorem (aka Hexagrammum Mysticum Theorem) states that if an arbitrary hexagon is inscribed in any conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, and pairs of opposite side
Side
Side was an ancient Greek city in Anatolia, in the region of Pamphylia, in what is now Antalya province, on the southern Mediterranean coast of Turkey...
s are extended until they meet, the three intersection
Line-line intersection
In Euclidean geometry, the intersection of a line and a line can be the empty set,a point, ora line. Distinguishing these cases, and finding the intersection point have use, for example, in computer graphics, motion planning, and collision detection....
points will lie on a straight line, the Pascal line of that configuration.

Related results
This theorem is a generalization of Pappus's hexagon theoremPappus's hexagon theorem
In mathematics, Pappus's hexagon theorem states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear...
– Pappus's theorem is the special case of a degenerate conic
Degenerate conic
In mathematics, a degenerate conic is a conic that fails to be an irreducible curve...
of two lines. Pascal's theorem is the polar reciprocal and projective dual of Brianchon's theorem
Brianchon's theorem
In geometry, Brianchon's theorem, named after Charles Julien Brianchon , is as follows. Let ABCDEF be a hexagon formed by six tangent lines of a conic section...
. It was discovered by Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
in 1639 when he was 16 years old.
A degenerate case of Pascal's Theorem is interesting indeed; given four points ABCD on a conic Γ, AB ∩ CD, BC ∩ DA, intersection of tangents at (A, C) and (B, D) are collinear (four points). This property can be proven independently using a property of pole-polar. If the conic is a circle, then another degenerate case tells us that for a triangle, the three points that appear as the intersection of a side line with the corresponding side line of the Gergonne triangle, are collinear, see Gergonne triangle.
Six is the minimum number of points on a conic about which special statements can be made, as five points determine a conic
Five points determine a conic
In geometry, just as two points determine a line , five points determine a conic . There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.Formally, given any five points in the plane in general...
.
The converse is the Braikenridge–Maclaurin theorem
Braikenridge–Maclaurin theorem
In geometry, the ', named for 18th century British mathematicians William Braikenridge and Colin Maclaurin , is the converse to Pascal's theorem. It states that if the 3 intersection points of the lines through three sides of a hexagon lie on a line, then the 6 vertices of the hexagon lie on a...
, named for 18th century British mathematicians William Braikenridge and Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
, which states that if the 3 intersection points of the lines through three sides of a hexagon lie on a line, then the 6 vertices of the hexagon lie on a conic; the conic may be degenerate, as in Pappus's theorem. The Braikenridge–Maclaurin theorem may be applied in the Braikenridge–Maclaurin construction, which is a synthetic
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
construction of the conic defined by five points, by varying the sixth point.
The theorem was generalized by Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
in 1847, as follows: suppose a polygon with 4n + 2 sides is inscribed in a conic section, and opposite pairs of sides are extended until they meet in 2n + 1 points. Then if 2n of those points lie on a common line, the last point will be on that line, too.
If six unordered points are given on a conic section, they can be connected into a hexagon in 60 different ways, resulting in 60 different instances of Pascal's theorem and 60 different Pascal lines.
As Thomas Kirkman proved in 1849, these 60 lines can be associated with 60 points in such a way that each point is on three lines and each line contains three points, forming a projective configuration. The 60 points formed in this way are now known as the Kirkman points .
Proofs
Pascal's own proof of the theorem has been lost, but there are various proofs for the theorem.It is sufficient to prove the theorem when the conic is a circle, because any (non-degenerate) conic can be reduced to a circle by a projective transformation; degenerate conics follow by continuity (the theorem is true for non-degenerate conics, and thus holds in the limit of degenerate conic).
A short elementary proof of Pascal's theorem in the case of a circle was found by , based on the proof in . This proof proves the theorem for circle and then generalizes it to conics.
We can infer the proof from existence of isogonal conjugate too. If we are to show that X = AB ∩ DE, Y = BC ∩ EF, Z = CD ∩ FA are collinear for conconical ABCDEF, then notice that ADY and CYF are similar, and that X and Z will correspond to the isogonal conjugate if we overlap the similar triangles. This means that angle DYX = angle CYZ, hence making XYZ collinear.
A short proof can be constructed using cross-ratio preservation. Projecting tetrad ABCE from D onto line AB, we obtain tetrad ABPX, and projecting tetrad ABCE from F onto line BC, we obtain tetrad QBCY. This therefore means that R(AB; PX) = R(QB; CY), where one of the points in the two tetrads overlap, hence meaning that other lines connecting the other three pairs must coincide to preserve cross ratio. Therefore XYZ are collinear.
Another proof for Pascal's theorem for a circle uses Menelaus' theorem
Menelaus' theorem
Menelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
repeatedly.
Dandelin, the geometer who discovered the celebrated Dandelin spheres
Dandelin spheres
In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin...
, came up with a beautiful proof using "3D lifting" technique that is analogous to the 3D proof of Desargues' theorem
Desargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
. The proof makes use of the property that for every conic section we can find a one-sheet hyperboloid which passes through the conic.
Also there exist a simple proof for Pascal's theorem for a circle uses Law of Sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
and similarity
Similarity
-Specific definitions:Different fields provide differing definitions of similarity:-In computer science:* string metric, aka string similarity* semantic similarity in computational linguistics-In other fields:...
.
Proof using cubic curves
Pascal's theorem has a short proof using the Cayley–Bacharach theorem that given any 8 points in general position, there is a unique ninth point such that all cubics through the first 8 also pass through the ninth point. In particular if 2 general cubics intersect in 8 points then any other cubic through the same 8 points meets the ninth point of intersection of the first two cubics. Pascal's theorem follows by taking the 8 points as the 6 points on the hexagon and two of the points (say, M and N in the figure) on the would-be Pascal line, and the ninth point as the third point (P in the figure). The first two cubics are two sets of 3 lines through the 6 points on the hexagon (for instance, the set AB, CD, EF, and the set BC, DE, FA), and the third cubic is the union of the conic and the line MN. Here the "ninth intersection" P cannot lie on the conic by genericity, and hence it lies on MN.The Cayley–Bacharach theorem is also used to prove that the group operation on cubic elliptic curves is associative. The same group operation can be applied on a cone if we choose a point E on the cone and a line MP in the plane. The sum of A and B is obtained by first finding the intersection point of line AB with MP, which is M. Next A and B add up to the second intersection point of the cone with line EM, which is D. Thus if Q is the second intersection point of the cone with line EN, then

Thus the group operation is associative. On the other hand, Pascal's theorem follows from the above associativity formula, and thus from the associativity of the group operation of elliptic curves by way of continuity.
Proof using Bézout's theorem
Suppose f is the cubic polynomial vanishing on the three lines through AB, CD, EF and g is the cubic vanishing on the other three lines BC, DE, FA. Pick a generic point P on the conic and choose λ so that the cubic h = f + λg vanishes on P. Then h = 0 is a cubic that has 7 points A, B, C, D, E, F, P in common with the conic. But by Bézout's theoremBézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
a cubic and a conic have at most 3 × 2 = 6 points in common, unless they have a common component. So the cubic h = 0 has a component in common with the conic which must be the conic itself, so h = 0 is the union of the conic and a line. It is now easy to check that this line is the Pascal line.
External links
- Interactive demo of Pascal's theorem (Java required) at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- 60 Pascal Lines (Java required) at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

