.gif)
Particle in a one-dimensional lattice (periodic potential)
Encyclopedia
In quantum mechanics
, the particle in a one-dimensional lattice is a problem that occurs in the model of a periodic crystal lattice
. The potential is caused by ion
s in the periodic structure of the crystal creating an electromagnetic field
so electrons are subject to a regular potential inside the lattice. This is an extension of the free electron model
that assumes zero potential inside the lattice.

The mathematical representation of the potential is a periodic function with a period a.
According to Bloch's theorem
, the wavefunction solution of the Schrödinger equation
when the potential is periodic, can be written as:

Where u(x) is a periodic function
which satisfies:

When nearing the edges of the lattice, there are problems with the boundary condition. Therefore, we can represent the ion lattice as a ring following the Born-von Karman boundary conditions. If L is the length of the lattice so that L >> a, then the number of ions in the lattice is so big, that when considering one ion, its surrounding is almost linear, and the wavefunction of the electron is unchanged.
So now, instead of two boundary conditions we get one circular boundary condition:

If N is the number of Ions in the lattice, then we have the relation: aN = L. Replacing in the boundary condition and applying Bloch's theorem will result in a quantization for k:



and William Penney
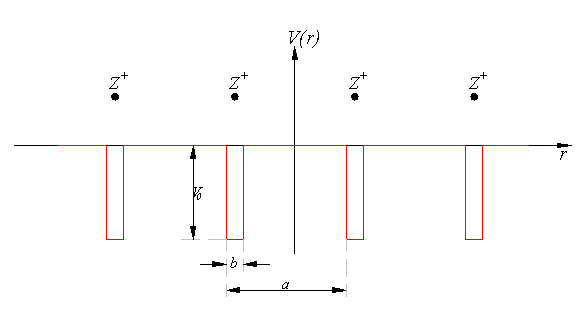
) is a simple, idealized quantum-mechanical system that consists of an infinite periodic array of rectangular potential barriers.
The potential function is approximated by a rectangular potential:
Using Bloch's theorem
, we only need to find a solution for a single period, make sure it is continuous and smooth, and to make sure the function u(x) is also continuous and smooth.
Considering a single period of the potential:
We have two regions here. We will solve for each independently:






To find u(x) in each region, we need to manipulate the electron's wavefunction:


And in the same manner:

To complete the solution we need to make sure the probability function is continuous and smooth, i.e.:

And that u(x) and u(x) are periodic

These conditions yield the following matrix:

For us not to have the trivial solution, the determinant of the matrix must be 0. This leads us to the following expression:

To further simplify the expression, we perform the following approximations:



The expression will now be:

Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the particle in a one-dimensional lattice is a problem that occurs in the model of a periodic crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. The potential is caused by ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s in the periodic structure of the crystal creating an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
so electrons are subject to a regular potential inside the lattice. This is an extension of the free electron model
Free electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
that assumes zero potential inside the lattice.
Problem definition
When talking about solid materials, the discussion is mainly around crystals - periodic lattices. Here we will discuss a 1D lattice of positive ions. Assuming the spacing between two ions is a, the potential in the lattice will look something like this:
The mathematical representation of the potential is a periodic function with a period a.
According to Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
, the wavefunction solution of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
when the potential is periodic, can be written as:

Where u(x) is a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
which satisfies:

When nearing the edges of the lattice, there are problems with the boundary condition. Therefore, we can represent the ion lattice as a ring following the Born-von Karman boundary conditions. If L is the length of the lattice so that L >> a, then the number of ions in the lattice is so big, that when considering one ion, its surrounding is almost linear, and the wavefunction of the electron is unchanged.
So now, instead of two boundary conditions we get one circular boundary condition:

If N is the number of Ions in the lattice, then we have the relation: aN = L. Replacing in the boundary condition and applying Bloch's theorem will result in a quantization for k:



Kronig–Penney model
The Kronig–Penney model (named after Ralph KronigRalph Kronig
Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...
and William Penney
William Penney, Baron Penney
William George Penney, Baron Penney OM, KBE PhD, DSc, , FRS, FRSE, FIC, Hon FCGI was a British mathematician who was responsible for the development of British nuclear technology, following World War II...
) is a simple, idealized quantum-mechanical system that consists of an infinite periodic array of rectangular potential barriers.
The potential function is approximated by a rectangular potential:

Using Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
, we only need to find a solution for a single period, make sure it is continuous and smooth, and to make sure the function u(x) is also continuous and smooth.
Considering a single period of the potential:
We have two regions here. We will solve for each independently:






To find u(x) in each region, we need to manipulate the electron's wavefunction:


And in the same manner:

To complete the solution we need to make sure the probability function is continuous and smooth, i.e.:

And that u(x) and u(x) are periodic

These conditions yield the following matrix:

For us not to have the trivial solution, the determinant of the matrix must be 0. This leads us to the following expression:

To further simplify the expression, we perform the following approximations:



The expression will now be:

See also
- Free electron modelFree electron modelIn solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
- Empty Lattice ApproximationEmpty Lattice ApproximationThe Empty Lattice Approximation is a theoretical electronic band structure model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move...
- Nearly-free electron modelNearly-free electron modelIn solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
- Crystal structureCrystal structureIn mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
- Mathieu functionMathieu functionIn mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...
External links
- "The Kronig-Penney Model" by Michael Croucher, an interactive calculation of 1d periodic potential band structure using MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
, from The Wolfram Demonstrations Project.

