.gif)
Transversal (geometry)
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a transversal is a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
that passes through two or more other lines in the same plane at different points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. When the lines are parallel
Parallel lines
Parallel Lines may refer to:*Parallel , two straight lines that never touch* Parallel Lines, an album by Blondie*Driver: Parallel Lines, a video game...
, as is often the case, a transversal produces several congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
and several supplementary angles
Supplementary angles
Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....
. When three lines in general position that form a triangle are cut by a transversal, the lengths of the six resulting segments satisfy Menelaus' theorem
Menelaus' theorem
Menelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
.
Terminology
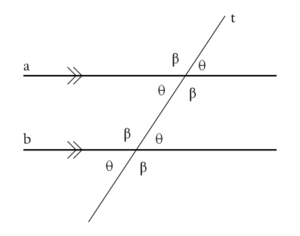
When a line l is the transversal of two lines m and n there are a total of eight angles formed. Names have been given to these angles and specific pairs. There are four interior angles defined as angles between m and n, and the remaining four are called exterior angles. A pair of angles, one formed by l and m and the other formed by l and n, are called corresponding angles if they are on the same side of l and on the same sides of m and n respectively. Similarly, a pair of angles are called alternating angles if they are on opposite sides of l and opposite sides of m and n.Related Theorems
EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's formulation of the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
may stated in terms of a transversal. Specifically, if the interior angles on the same side of the transversal are less than two right angles then lines must intersect. In fact, Euclid uses the same phrase in Greek that is usually translated as "transversal".
Euclid's Proposition 27 states that if a transversal intersects two lines so that alternate interior angles are congruent, then the lines are parallel. Euclid proves this by contradiction: If the lines are not parallel then they must intersect and a triangle is formed. Then one of the alternate angles is an exterior angle equal to the other angle which is an opposite interior angle in the triangle. This contradicts Proposition 16 which states that an exterior angle on a triangle is always greater than the opposite interior angles.
Euclid's Proposition 28 extends this result in two ways. First, if a transversal intersects two lines so that corresponding angles are congruent, then the lines are parallel. Second, if a transversal intersects two lines so that interior angles on the same side of the transversal are supplementary, then the lines are parallel. These follow from the previous proposition by applying the fact than opposite angles on intersecting lines equal (Prop. 15) and that adjacent angles on a line are supplementary (Prop. 13). As noted by Proclus
Proclus
Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...
, Euclid gives only three of a possible six such criteria for parallel lines.
Euclid's Proposition 29 is a converse to the previous two. First, if a transversal intersects two parallel lines, then the alternate interior angles are congruent. If not then one is greater than the other, which implies it's supplement is less than the supplement of the other angle. This implies that there are interior angles on the same side of the transversal which are less than two right angles, contradicting the fifth postulate. The proposition continues by stating that in a transversal of two parallel lines, corresponding angles are congruent and interior angles on the same side equal two right angles. These statements follow in the same way that Prop. 28 follows from Prop. 27.
Euclid's proof makes essential use of fifth postulate, however modern treatments of geometry use Playfair's axiom
Playfair's axiom
Playfair's axiom is a geometrical axiom, intended to replace the fifth postulate of Euclides :Given a line and a point not on it, at most one parallel to the given line can be drawn through the point....
instead. To prove proposition 29 assuming Playfair's axiom, let a transversal cross two parallel lines and suppose alternate interior angles are not equal. Draw a third line through the point where the transversal crosses the first line, but with angle equal to the angle the transversal makes with the second angle. This produces two different lines through a point both parallel to another line, contradicting the axiom.
External links
- Transversal and Angles Interactive transversal with color coded angles (corresponding, alternate interior etc..)
- Transversal definition With interactive animation
- The alternate interior angles associated with a transversal With interactive animation
- The alternate exterior angles associated with a transversal With interactive animation
- Corresponding angles associated with a transversal line With interactive animations
- Exterior angles associated with a transversal line With interactive animation

