
Paradoxical set
Encyclopedia

Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a paradoxical set is a set that has a paradoxical decomposition. A paradoxical decomposition of a set is a partitioning
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the set into exactly two subsets, along with an appropriate group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of functions that operate on some universe (of which the set in question is a subset), such that each partition can be mapped back onto the entire set using only finitely many distinct functions (or compositions thereof) to accomplish the mapping. Since a paradoxical set as defined requires a suitable group
 , it is said to be
, it is said to be  -paradoxical, or paradoxical with respect to
-paradoxical, or paradoxical with respect to  .
.Paradoxical sets exist as a consequence of the Axiom of Infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
. Admitting infinite classes as sets is sufficient to allow paradoxical sets.
Natural numbers
An example of a paradoxical set is the natural numbers. They are paradoxical with respect to the group of functions generated by the natural function
generated by the natural function  :
: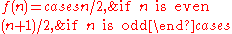
Split the natural numbers into the odds and the evens. The function
 maps both sets onto the whole of
maps both sets onto the whole of  . Since only finitely many functions were needed, the naturals are
. Since only finitely many functions were needed, the naturals are  -paradoxical. This example does not work: the natural function is not injective, and as such has no well defined inverse. Therefore it does not generate a group of functions.
-paradoxical. This example does not work: the natural function is not injective, and as such has no well defined inverse. Therefore it does not generate a group of functions.Banach–Tarski paradox
The most famous, and indeed motivational, example of paradoxical sets is the Banach–Tarski paradoxBanach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
, which divides the sphere into paradoxical sets for the special orthogonal group. This result depends on the axiom of choice.

