
Pairing heap
Encyclopedia
A pairing heaps is a type of heap
data structure
with relatively simple implementation and excellent practical amortized performance. However, it has proven very difficult to determine the precise asymptotic running time of pairing heaps.
Pairing heaps are heap ordered multiway tree
s. Describing the various heap operations is relatively simple (in the following we assume a min-heap):
The amortized time per delete-min is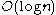 . The operations find-min, merge, and insert are
. The operations find-min, merge, and insert are  and decrease-key takes
and decrease-key takes 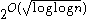 amortized time.
amortized time.
Fredman
proved that the amortized time per decrease-key is at least .
.
Although this is worse than other priority queue algorithms such as Fibonacci heap
s, which perform decrease-key in amortized time, the performance in practice is excellent. Stasko
amortized time, the performance in practice is excellent. Stasko
and Vitter and Moret and Shapiro conducted experiments on pairing heaps and other heap data structures. They concluded that the pairing heap is as fast as, and often faster than, other efficient data structures like the binary heap
s.
type PairingHeap[Elem] = Empty | Heap(elem: Elem, subheaps: List[PairingHeap[Elem]])
function find-min(heap)
if heap Empty
error
else
return heap.elem
function merge(heap1, heap2)
if heap1 Empty
return heap2
elsif heap2 Empty
return heap1
elsif heap1.elem < heap2.elem
return Heap(heap1.elem, heap2 :: heap1.subheaps)
else
return Heap(heap2.elem, heap1 :: heap2.subheaps)
function insert(elem, heap)
return merge(Heap(elem, []), heap)
function delete-min(heap)
if heap Empty
error
elsif length(heap.subheaps) 0
1
return heap.subheaps[0]
else
return merge-pairs(heap.subheaps)
This uses the auxiliary function merge-pairs:
function merge-pairs(l)
if length(l) 0
1
return l[0]
else
return merge(merge(l[0], l[1]), merge-pairs(l[2.. ]))
That this does indeed implement the described two-pass left-to-right then right-to-left merging strategy can be seen from this reduction:
merge-pairs([H1, H2, H3, H4, H5, H6, H7])
=> merge(merge(H1, H2), merge-pairs([H3, H4, H5, H6, H7]))
# merge H1 and H2 to H12, then the rest of the list
=> merge(H12, merge(merge(H3, H4), merge-pairs([H5, H6, H7])))
# merge H3 and H4 to H34, then the rest of the list
=> merge(H12, merge(H34, merge(merge(H5, H6), merge-pairs([H7]))))
# merge H5 and H5 to H56, then the rest of the list
=> merge(H12, merge(H34, merge(H56, H7)))
# switch direction, merge the last two resulting heaps, giving H567
=> merge(H12, merge(H34, H567))
# merge the last two resulting heaps, giving H34567
=> merge(H12, H34567)
# finally, merge the first merged pair with the result of merging the rest
=> H1234567
Heap (data structure)
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if B is a child node of A, then key ≥ key. This implies that an element with the greatest key is always in the root node, and so such a heap is sometimes called a max-heap...
data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
with relatively simple implementation and excellent practical amortized performance. However, it has proven very difficult to determine the precise asymptotic running time of pairing heaps.
Pairing heaps are heap ordered multiway tree
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
s. Describing the various heap operations is relatively simple (in the following we assume a min-heap):
- find-min: simply return the top element of the heap.
- merge: compare the two root elements, the smaller remains the root of the result, the larger element and its subtree is appended as a child of this root.
- insert: create a new heap for the inserted element and merge into the original heap.
- decrease-key (optional): remove the subtree rooted at the key to be decreased then merge it with the heap.
- delete-min: remove the root and merge its subtrees. Various strategies are employed.
The amortized time per delete-min is
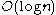 . The operations find-min, merge, and insert are
. The operations find-min, merge, and insert are  and decrease-key takes
and decrease-key takes 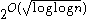 amortized time.
amortized time.Fredman
Michael Fredman
Michael Lawrence Fredman is a professor at the Computer Science Department at Rutgers University, United States. He got his Ph. D. degree from Stanford University in 1972 under the supervision of Donald Knuth. He was a member of the mathematics department at the Massachusetts Institute of...
proved that the amortized time per decrease-key is at least
 .
.Although this is worse than other priority queue algorithms such as Fibonacci heap
Fibonacci heap
In computer science, a Fibonacci heap is a heap data structure consisting of a collection of trees. It has a better amortized running time than a binomial heap. Fibonacci heaps were developed by Michael L. Fredman and Robert E. Tarjan in 1984 and first published in a scientific journal in 1987...
s, which perform decrease-key in
 amortized time, the performance in practice is excellent. Stasko
amortized time, the performance in practice is excellent. StaskoJohn Stasko
John Thomas Stasko III is a Professor in and the Associate Chair of the School of Interactive Computing in the College of Computing at the Georgia Tech, where he joined the faculty in 1989. He also is one of the founding members of the Graphics, Visualization, and Usability Center there...
and Vitter and Moret and Shapiro conducted experiments on pairing heaps and other heap data structures. They concluded that the pairing heap is as fast as, and often faster than, other efficient data structures like the binary heap
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
s.
Implementation
A pairing heap is either an empty heap, or a pair consisting of a root element and a possibly empty list of pairing heaps. The heap ordering property requires that all the root elements of the subheaps in the list are not smaller than the root element of the heap. The following description assumes a purely functional heap that does not support the decrease-key operation.type PairingHeap[Elem] = Empty | Heap(elem: Elem, subheaps: List[PairingHeap[Elem]])
find-min
The function find-min simply returns the root element of the heap:function find-min(heap)
if heap Empty
error
else
return heap.elem
merge
Merging with an empty heap returns the other heap, otherwise a new heap is returned that has the minimum of the two root elements as its root element and just adds the heap with the larger root to the list of subheaps:function merge(heap1, heap2)
if heap1 Empty
return heap2
elsif heap2 Empty
return heap1
elsif heap1.elem < heap2.elem
return Heap(heap1.elem, heap2 :: heap1.subheaps)
else
return Heap(heap2.elem, heap1 :: heap2.subheaps)
insert
The easiest way to insert an element into a heap is to merge the heap with a new heap containing just this element and an empty list of subheaps:function insert(elem, heap)
return merge(Heap(elem, []), heap)
delete-min
The only non-trivial fundamental operation is the deletion of the minimum element from the heap. The standard strategy first merges the subheaps in pairs (this is the step that gave this datastructure its name) from left to right and then merges the resulting list of heaps from right to left:function delete-min(heap)
if heap Empty
error
elsif length(heap.subheaps)
0
return Empty
elsif length(heap.subheaps)
1return heap.subheaps[0]
else
return merge-pairs(heap.subheaps)
This uses the auxiliary function merge-pairs:
function merge-pairs(l)
if length(l)
0
return Empty
elsif length(l)
1return l[0]
else
return merge(merge(l[0], l[1]), merge-pairs(l[2.. ]))
That this does indeed implement the described two-pass left-to-right then right-to-left merging strategy can be seen from this reduction:
merge-pairs([H1, H2, H3, H4, H5, H6, H7])
=> merge(merge(H1, H2), merge-pairs([H3, H4, H5, H6, H7]))
# merge H1 and H2 to H12, then the rest of the list
=> merge(H12, merge(merge(H3, H4), merge-pairs([H5, H6, H7])))
# merge H3 and H4 to H34, then the rest of the list
=> merge(H12, merge(H34, merge(merge(H5, H6), merge-pairs([H7]))))
# merge H5 and H5 to H56, then the rest of the list
=> merge(H12, merge(H34, merge(H56, H7)))
# switch direction, merge the last two resulting heaps, giving H567
=> merge(H12, merge(H34, H567))
# merge the last two resulting heaps, giving H34567
=> merge(H12, H34567)
# finally, merge the first merged pair with the result of merging the rest
=> H1234567
External links
- Louis Wasserman discusses pairing heaps and their implementation in HaskellHaskell (programming language)Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
in The Monad Reader, Issue 16 (pp. 37–52). - pairing heaps, Sartaj SahniSartaj SahniProf. Sartaj Kumar Sahni is an Indian computer scientist, now based in the USA, and is one of the pioneers in the field of data structures. He is a distinguished professor in the Department of Computer and Information Science and Engineering at the University of Florida.- Biography :Sahni received...

