P system
Encyclopedia
A P system is a computational model in the field of computer science
that performs calculation
s using a biologically-inspired process. They are based upon the structure of biological cells
, abstracting from the way in which chemicals
interact and cross cell membranes. The concept was first introduced in a 1998 report by the computer scientist Gheorghe Păun
, whose last name is the origin of the letter P
in 'P Systems'. Variations on the P system model led to the formation of a branch of research known as 'membrane computing
.'
Although inspired by biology, the primary research interest in P systems is concerned with their use as a computational model, rather than for biological modeling
, although this is also being investigated.
Just as in a biological cell, where a chemical reaction may only take place upon the chance event that the required chemical molecule
s collide and interact (possibly also with a catalyst), the rules in a P system are applied at random. This causes the computation to proceed in a non-deterministic manner, often resulting in multiple solutions being encountered if the computation is repeated.
A P system continues until it reaches a state where no further reactions are possible. At this point the result of the computation is all those chemicals that have been passed outside of the outermost membrane, or otherwise those passed into a designated 'result' membrane.
and symbols resulting from a rule may cross them. A membrane (but not the container membrane) may also “dissolve”, in which case its content, except for rules (which are lost), migrate into the membrane in which it was contained.
Some P system variants allow for a membrane to divide, possess a charge
or have varying permeability
by changing membrane thickness.
letter. The symbol content of a membrane is therefore represented by a string of letters. Because the multiplicity of symbols in a region matters, multisets are commonly used to represent the symbol content of a region.
Special case symbols exist, for example a lower case delta
(δ) is often used to initiate the dissolving of a membrane, and this will only ever be found in the output of a rule: upon being encountered it invokes a reaction, and is used in the process.
,” they are simply a requirement for it to occur.
There are three (in the basic P system model) distinct ways in a rule may handle its output objects. Usually the output objects are passed into the current membrane (the same membrane in which the rule and the inputs reside), known as a here rule. However there are two modifiers which can be specified upon output objects when rules are defined, in and out. The in modifier causes the object to be passed to one of the current membrane’s children (travelling inwards relative to the structure of the P system), chosen at random
during the computation. The out modifier causes the object to be passed out of the current membrane and into either its parent membrane or to a sibling membrane, specified during specification of the P system.
Working through step-by-step, a computation halts when no further evolution can take place (i.e. when no rules are able to be applied). At this point whatever objects have been passed to the environment, or into a designated 'result' membrane, are counted as the result of the computation.
Outputs are not passed immediately into membranes because this would contravene the maximally parallel nature of rule application, instead they are distributed after all possible rules have been applied.
Consider a membrane containing only a single "a" symbol, and the two rules a → ab and a → aδ. As both rules rely on an “a” symbol being present, of which there is only one, the first step of computation will allow either the first or second rule to be applied, but not both. The two possible results of this step are very different:
As a model for computation, P systems offer the attractive possibility of solving NP-complete
problems in less-than exponential time. Some P system variants are known to be capable of solving the SAT
(boolean satisfiability) problem in linear time and, owing to all NP-complete problems being equivalent
, this capability then applies all such problems. As there is no current method of directly implementing a P system in its own right, their functionality is instead emulated, solving NP-complete problems in linear time remains theoretical. However, it has also been proven that any deterministic P system may be simulated on a Turing Machine
in polynomial time.
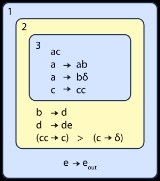
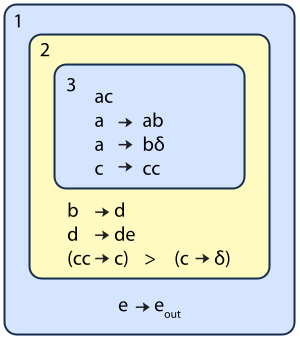The image shown depicts the initial state of a P system with three membranes. Because of their hierarchical nature, P systems are often depicted graphically with drawings that resemble Venn diagram
s or David Harel
's Higraph
(see Statechart).
The outermost membrane, 1, is the container membrane for this P system and contains a single out rule. Membrane 2 contains four here rules, with two in a priority relationship: cc → c will always be applied in preference to c → cδ. The delta symbol represents the special “dissolve” symbol. The innermost membrane, 3, contains a set of symbols (“ac”) and three rules, of type here. In this initial state no rules outside of membrane 3 are applicable: there are no
symbols outside of that membrane. However, during evolution of the system, as objects are passed between membranes, the rules in other membranes will become active.
Notice the maximally parallel behaviour of rule application leading to the same rule being applied twice during one step.
Membrane 3 now dissolves, as the dissolve symbol (δ) has been encountered and all object content from this membrane passes into membrane 2.
Notice that the priority over c → δ has been lifted now the required inputs for cc→ c no longer exist. Membrane 2 now dissolves, and all object content passes
to membrane 1.
assignments of objects to rules is possible. The result of the computation is four "e" symbols.
The only non-determanistic choices occurred during steps 1 and 2, when choosing where to assign the solitary "a" symbol. Consider the case where "a" is assigned to a → bδ during step 1: upon membrane 3 dissolving only a single "b" and two "c" objects would exist, leading to the creation of only a single "e" object to eventually be passed out as the computation’s result.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that performs calculation
Calculation
A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...
s using a biologically-inspired process. They are based upon the structure of biological cells
Cell (biology)
The cell is the basic structural and functional unit of all known living organisms. It is the smallest unit of life that is classified as a living thing, and is often called the building block of life. The Alberts text discusses how the "cellular building blocks" move to shape developing embryos....
, abstracting from the way in which chemicals
Chemical substance
In chemistry, a chemical substance is a form of matter that has constant chemical composition and characteristic properties. It cannot be separated into components by physical separation methods, i.e. without breaking chemical bonds. They can be solids, liquids or gases.Chemical substances are...
interact and cross cell membranes. The concept was first introduced in a 1998 report by the computer scientist Gheorghe Păun
Gheorghe Paun
Gheorghe Păun is a computer scientist from Romania, prominent for work on membrane computing and the P system.Păun studied mathematics at the University of Bucharest, obtaining an MSc. in 1974 and a PhD in 1977. He has been a researcher at the Institute of Mathematics of the Romanian Academy since...
, whose last name is the origin of the letter P
P
P is the sixteenth letter of the basic modern Latin alphabet.-Usage:In English and most other European languages, P is a voiceless bilabial plosive. Both initial and final Ps can be combined with many other discrete consonants in English words...
in 'P Systems'. Variations on the P system model led to the formation of a branch of research known as 'membrane computing
Membrane computing
Membrane computing is an area within computer science that seeks to discover new computational models from the study of biological cells, particular of the cellular membranes. It is a sub-task of creating a cellular model....
.'
Although inspired by biology, the primary research interest in P systems is concerned with their use as a computational model, rather than for biological modeling
Mathematical biology
Mathematical and theoretical biology is an interdisciplinary scientific research field with a range of applications in biology, medicine and biotechnology...
, although this is also being investigated.
Informal description
A P system is defined as a series of membranes containing chemicals (in finite quantities), catalysts and rules which determine possible ways in which chemicals may react with one another to form products. Rules may also cause chemicals to pass through membranes or even cause membranes to dissolve.Just as in a biological cell, where a chemical reaction may only take place upon the chance event that the required chemical molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s collide and interact (possibly also with a catalyst), the rules in a P system are applied at random. This causes the computation to proceed in a non-deterministic manner, often resulting in multiple solutions being encountered if the computation is repeated.
A P system continues until it reaches a state where no further reactions are possible. At this point the result of the computation is all those chemicals that have been passed outside of the outermost membrane, or otherwise those passed into a designated 'result' membrane.
Components of a P system
Although many varieties of P system exist, most share the same basic components. Each element has a specific role to play, and each has a founding in the biological cell architecture upon which P systems are based.The environment
The environment is the surroundings of the P system. In the initial state of a P system it contains only the container-membrane, and while the environment can never hold rules, it may have objects passed into it during the computation. The objects found within the environment at the end of the computation constitute all or part of its “result.”Membranes
Membranes are the main “structures” within a P system. A membrane is a discrete unit which can contain a set of objects (symbols/catalysts), a set of rules, and a set of other membranes contained within. The outermost membrane, held within the environment, is often referred to as the 'container membrane' or 'skin membrane'. As implied to by their namesake, membranes are permeableSemipermeable membrane
A semipermeable membrane, also termed a selectively permeable membrane, a partially permeable membrane or a differentially permeable membrane, is a membrane that will allow certain molecules or ions to pass through it by diffusion and occasionally specialized "facilitated diffusion".The rate of...
and symbols resulting from a rule may cross them. A membrane (but not the container membrane) may also “dissolve”, in which case its content, except for rules (which are lost), migrate into the membrane in which it was contained.
Some P system variants allow for a membrane to divide, possess a charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
or have varying permeability
Semipermeable membrane
A semipermeable membrane, also termed a selectively permeable membrane, a partially permeable membrane or a differentially permeable membrane, is a membrane that will allow certain molecules or ions to pass through it by diffusion and occasionally specialized "facilitated diffusion".The rate of...
by changing membrane thickness.
Symbols
Symbols represent chemicals which may react with other chemicals to form some product. In a P system each type of symbol is typically represented by a differentletter. The symbol content of a membrane is therefore represented by a string of letters. Because the multiplicity of symbols in a region matters, multisets are commonly used to represent the symbol content of a region.
Special case symbols exist, for example a lower case delta
Delta (letter)
Delta is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter Dalet...
(δ) is often used to initiate the dissolving of a membrane, and this will only ever be found in the output of a rule: upon being encountered it invokes a reaction, and is used in the process.
Catalysts
Catalysts are similar to their namesakes in chemistry. They are represented and used in the same way as symbols, but are never consumed during a “reactionChemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
,” they are simply a requirement for it to occur.
Rules
Rules represent a possible chemical reaction within a membrane, causing it to evolve to a new state. A rule has a required set of input objects (symbols or catalysts) which must be present in order for it to be applied. If the required objects are present, it consumes them and produces a set of output objects. A rule may also be specified to have a priority over other rules, in which case less dominant rules will only be applied when it is not possible to apply a more dominant rule (i.e. the required inputs are not present).There are three (in the basic P system model) distinct ways in a rule may handle its output objects. Usually the output objects are passed into the current membrane (the same membrane in which the rule and the inputs reside), known as a here rule. However there are two modifiers which can be specified upon output objects when rules are defined, in and out. The in modifier causes the object to be passed to one of the current membrane’s children (travelling inwards relative to the structure of the P system), chosen at random
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
during the computation. The out modifier causes the object to be passed out of the current membrane and into either its parent membrane or to a sibling membrane, specified during specification of the P system.
Computation process
A computation works from an initial starting state towards an end state through a number of discrete steps. Each step involves iterating through all membranes in the P system and the application of rules, which occurs in both a maximally parallel and non-deterministic manner.Working through step-by-step, a computation halts when no further evolution can take place (i.e. when no rules are able to be applied). At this point whatever objects have been passed to the environment, or into a designated 'result' membrane, are counted as the result of the computation.
Rule application
At each step of a computation an object may only be used once, as they are consumed by rules when applied. The method of applying a rule within a membrane is as follows:- Assign symbols from a membrane’s content to the rule’s inputs
- If all inputs are satisfied, remove all assigned symbols from membrane
- Create output symbols and hold until all rule assignment, for all membranes, has taken place.
- Add output symbols to targeted membranes.
- Dissolve membranes as necessary
Outputs are not passed immediately into membranes because this would contravene the maximally parallel nature of rule application, instead they are distributed after all possible rules have been applied.
Non-deterministic application
The order of rule application is chosen at random. Rule application order can have a significant effect on which rules may be applied at any given time, and the outcome of a step of execution.Consider a membrane containing only a single "a" symbol, and the two rules a → ab and a → aδ. As both rules rely on an “a” symbol being present, of which there is only one, the first step of computation will allow either the first or second rule to be applied, but not both. The two possible results of this step are very different:
- The membrane carries over to the next step of the computation with both an "a" symbol and a "b" symbol present, and again one of the two rules is randomly assigned to the "a" symbol.
- The membrane dissolves and a single "a" symbol is passed out to the containing membrane.
Maximally parallel application
This is a property of rule application whereby all possible rule assignments must take place during every step of the computation. In essence this means that the rule a → aa has the effect of doubling the number of "a" symbols in its containing membrane each step, because the rule is applied to every occurrence of an "a" symbol present.As a computational model
Most P systems variants are computationally universal. This extends even to include variants that do not use rule priorities, usually a fundamental aspect of P systems.As a model for computation, P systems offer the attractive possibility of solving NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problems in less-than exponential time. Some P system variants are known to be capable of solving the SAT
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
(boolean satisfiability) problem in linear time and, owing to all NP-complete problems being equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
, this capability then applies all such problems. As there is no current method of directly implementing a P system in its own right, their functionality is instead emulated, solving NP-complete problems in linear time remains theoretical. However, it has also been proven that any deterministic P system may be simulated on a Turing Machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
in polynomial time.
Example computation
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
s or David Harel
David Harel
David Harel is a professor of computer science at the Weizmann Institute of Science in Israel. Born in London, England, he was Dean of the Faculty of Mathematics and Computer Science at the institute for seven years.-Biography:...
's Higraph
Higraph
A higraph is a diagramming object that formalizes relations into a visual structure, it was developed by David Harel in 1988. Higraphs extend mathematical graphs by including notions of depth and orthogonality. In particular, nodes in a higraph can contain other nodes inside them, creating a...
(see Statechart).
The outermost membrane, 1, is the container membrane for this P system and contains a single out rule. Membrane 2 contains four here rules, with two in a priority relationship: cc → c will always be applied in preference to c → cδ. The delta symbol represents the special “dissolve” symbol. The innermost membrane, 3, contains a set of symbols (“ac”) and three rules, of type here. In this initial state no rules outside of membrane 3 are applicable: there are no
symbols outside of that membrane. However, during evolution of the system, as objects are passed between membranes, the rules in other membranes will become active.
Computation
Because of the non-deterministic nature of P systems, there are many different paths of computation a single P system is capable of, leading to different results. The following is one possible path of computation for the P system depicted.Step 1
From the initial configuration only membrane 3 has any object content: "ac"- "c" is assigned to c → cc
- "a" is assigned to a → ab
Step 2
Membrane 3 now contains: "abcc"- "a" is assigned to a → bδ
- "c" is assigned to c → cc
- "c" is assigned to c → cc
Notice the maximally parallel behaviour of rule application leading to the same rule being applied twice during one step.
Membrane 3 now dissolves, as the dissolve symbol (δ) has been encountered and all object content from this membrane passes into membrane 2.
Step 3
Membrane 2 now contains: “bbcccc”- "b" is assigned to b → d
- "b" is assigned to b → d
- "cc" is assigned to cc → c
- "cc" is assigned to cc → c
Step 4
Membrane 2 now contains: "ddcc"- "d" is assigned to d → de
- "d" is assigned to d → de
- "cc" is assigned to cc → c
Step 5
Membrane 2 now contains: “dedec”- "d" is assigned to d → de
- "d" is assigned to d → de
- "c" is assigned to c → δ
Notice that the priority over c → δ has been lifted now the required inputs for cc→ c no longer exist. Membrane 2 now dissolves, and all object content passes
to membrane 1.
Step 6
Membrane 1 now contains: “deedee”- "e” is assigned to e → eout
- "e” is assigned to e → eout
- "e” is assigned to e → eout
- "e” is assigned to e → eout
Computation halts
Membrane 1 now contains: "dd" and, due to the out rule e → eout, the environment contains: "eeee." At this point the computation halts as no furtherassignments of objects to rules is possible. The result of the computation is four "e" symbols.
The only non-determanistic choices occurred during steps 1 and 2, when choosing where to assign the solitary "a" symbol. Consider the case where "a" is assigned to a → bδ during step 1: upon membrane 3 dissolving only a single "b" and two "c" objects would exist, leading to the creation of only a single "e" object to eventually be passed out as the computation’s result.
See also
- Cell (biology)Cell (biology)The cell is the basic structural and functional unit of all known living organisms. It is the smallest unit of life that is classified as a living thing, and is often called the building block of life. The Alberts text discusses how the "cellular building blocks" move to shape developing embryos....
- Biologically inspired computing
- Formal languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
- HypergraphHypergraphIn mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
- Systems biologySystems biologySystems biology is a term used to describe a number of trends in bioscience research, and a movement which draws on those trends. Proponents describe systems biology as a biology-based inter-disciplinary study field that focuses on complex interactions in biological systems, claiming that it uses...