
PPAD (complexity)
Encyclopedia
PPAD is a complexity class
introduced by Christos Papadimitriou
in 1994. PPAD is a subclass of TFNP
based on functions that can be shown to be total by a parity argument. The class attracted significant attention in the field of algorithmic game theory
because it contains the problem of computing a Nash equilibrium
, and this problem was shown by Chen and Deng in 2005 to be complete for the class.
PPAD is a class of problems that are believed to be hard, but obtaining PPAD-completeness is a weaker evidence of intractability than that of obtaining NP-completeness. It could still be the case that PPAD is the same class as P, and still have that P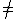 NP, though it seems unlikely. Examples of PPAD-complete problems include finding Nash equilibria, Brouwer and Borsuk-Ulam fixpoints, the cutting sandwich problem
NP, though it seems unlikely. Examples of PPAD-complete problems include finding Nash equilibria, Brouwer and Borsuk-Ulam fixpoints, the cutting sandwich problem
, finding Arrow Debreu equilibria in markets and more (The Complexity of Finding Nash Equilibria, Papadimitriou).
, the class of function problem
s in FNP
that are guaranteed to be total. Its formal definition may be given as follows:
Subclasses of TFNP are defined based on the type of mathematical proof used to prove that a solution always exists. Informally, PPAD is the subclass of TFNP where the guarantee that there exists a y such that P(x,y) holds is based on a parity argument on a directed graph. The class is formally defined by specifying one of its complete problems, known as End-Of-The-Line:
Such a t must exist if an s does, because the structure of G means that vertices with only one neighbour come in pairs. In particular, given s, we can find such a t at the other end of the string starting at s. (Note that this may take exponential time if we just evaluate f repeatedly.)
(the corresponding class of parity arguments for undirected graphs) which is contained in TFNP. PPAD is also contained in (but not known to be equal to) PPP
, another subclass of TFNP. It contains CLS.
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
introduced by Christos Papadimitriou
Christos Papadimitriou
Christos Harilaos Papadimitriou is a Professor in the Computer Science Division at the University of California, Berkeley, United States...
in 1994. PPAD is a subclass of TFNP
TFNP
In computational complexity theory, the complexity class TFNP is a subclass of FNP where a solution is guaranteed to exist. It stands for "Total Function Nondeterministic Polynomial."...
based on functions that can be shown to be total by a parity argument. The class attracted significant attention in the field of algorithmic game theory
Algorithmic game theory
Algorithmic game theory is an area in the intersection of game theory and algorithm design, whose objective is to design algorithms in strategic environments. Typically, in Algorithmic Game Theory problems, the input to a given algorithm is distributed among many players who have a personal...
because it contains the problem of computing a Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
, and this problem was shown by Chen and Deng in 2005 to be complete for the class.
PPAD is a class of problems that are believed to be hard, but obtaining PPAD-completeness is a weaker evidence of intractability than that of obtaining NP-completeness. It could still be the case that PPAD is the same class as P, and still have that P
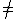 NP, though it seems unlikely. Examples of PPAD-complete problems include finding Nash equilibria, Brouwer and Borsuk-Ulam fixpoints, the cutting sandwich problem
NP, though it seems unlikely. Examples of PPAD-complete problems include finding Nash equilibria, Brouwer and Borsuk-Ulam fixpoints, the cutting sandwich problemHam sandwich theorem
In measure theory, a branch of mathematics, the ham sandwich theorem, also called the Stone–Tukey theorem after Arthur H. Stone and John Tukey, states that given measurable "objects" in -dimensional space, it is possible to divide all of them in half with a single -dimensional hyperplane...
, finding Arrow Debreu equilibria in markets and more (The Complexity of Finding Nash Equilibria, Papadimitriou).
Definition
PPAD is a subset of the class TFNPTFNP
In computational complexity theory, the complexity class TFNP is a subclass of FNP where a solution is guaranteed to exist. It stands for "Total Function Nondeterministic Polynomial."...
, the class of function problem
Function problem
In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...
s in FNP
FNP (complexity)
In computational complexity theory, the complexity class FNP is the function problem extension of the decision problem class NP. The name is somewhat of a misnomer, since technically it is a class of binary relations, not functions, as the following formal definition explains:This definition does...
that are guaranteed to be total. Its formal definition may be given as follows:
- A binary relation P(x,y) is in TFNP if and only if there is a deterministic polynomial time algorithm that can determine whether P(x,y) holds given both x and y, and for every x, there exists a y such that P(x,y) holds.
Subclasses of TFNP are defined based on the type of mathematical proof used to prove that a solution always exists. Informally, PPAD is the subclass of TFNP where the guarantee that there exists a y such that P(x,y) holds is based on a parity argument on a directed graph. The class is formally defined by specifying one of its complete problems, known as End-Of-The-Line:
- G is a (possibly exponentially large) directed graph with no isolated vertices, and with every vertexVertex (graph theory)In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
having at most one predecessor and one successor. G is specified by giving a polynomial-time computable function f(v) (polynomial in the size of v) that returns the predecessor and successor (if they exist) of the vertex v. Given a vertex s in G with no predecessor, find a vertex t≠s with no predecessor or no successor. (The input to the problem is the source vertex s and the function f(v)). In other words, we want any source or sink of the directed graph other than s.
Such a t must exist if an s does, because the structure of G means that vertices with only one neighbour come in pairs. In particular, given s, we can find such a t at the other end of the string starting at s. (Note that this may take exponential time if we just evaluate f repeatedly.)
Relationship to other complexity classes
PPAD is contained in (but not known to be equal to) PPAPPA (complexity)
PPA is a complexity class, standing for "Polynomial Parity Argument" . Introduced by Christos Papadimitriou in 1994 , PPA is a subclass of TFNP...
(the corresponding class of parity arguments for undirected graphs) which is contained in TFNP. PPAD is also contained in (but not known to be equal to) PPP
PPP (complexity)
PPP is a complexity class, standing for "Polynomial Pigeonhole Principle". Introduced by Christos Papadimitriou in 1994 , PPP is a subclass of TFNP. It is a class of search problems that can be shown to be total by an application of the pigeonhole principle.PPP is defined as follows...
, another subclass of TFNP. It contains CLS.
Other notable complete problems
- Finding the Nash equilibriumNash equilibriumIn game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
on a 2-player game or a game with any number of players. - Finding a three-colored point in Sperner's LemmaSperner's lemmaIn mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...
.

