Ostrowski's theorem
Encyclopedia
Ostrowski's theorem, due to Alexander Ostrowski
(1916), states that any non-trivial absolute value
on the rational number
s Q is equivalent to either the usual real absolute value or a p-adic
absolute value.
s
and 
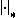on a field
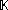are defined to be equivalent if there exists a real number c > 0 such that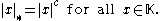
Observe that this is stronger than saying that the two absolute-value structures are topologically isomorphic.
The trivial absolute value on any field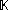
is defined to be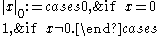
The real absolute value on the rationals
is the normal absolute value on the reals, defined to be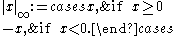
This is sometimes written with a subscript 1 instead of infinity.
For a prime number
p, the p-adic absolute value on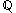
is defined as follows: any non-zero rational x, can be written uniquely as
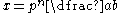with a, b and p pairwise coprime
and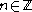
some integer; so we define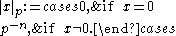
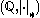. We consider two cases, (i) 
and (ii) 
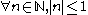. It suffices for us to consider the valuation of integers greater than one. For if we find some 
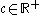for which 
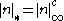for all naturals greater than one; then this relation trivially holds for 0 and 1, and for positive rationals
;
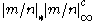and for negative rationals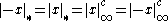
.
Case I:
Consider the following calculation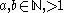. Let 
. Let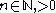 
. Expressing 
in base
yields 
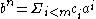, where each 
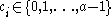and 
.
Then we see, by the properties of an absolute value:
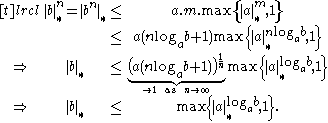
Now choose
such that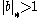 
.Using this in the above ensures that 
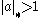regardless of the choice of 
(else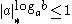 
implying 
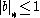). Thus for any choice of 
above, we get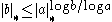 
, i.e. 
.
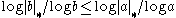By symmetry, this inequality is an equality.
Since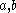
were arbitrary, there is a constant, 
for which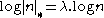 
,
i.e.
for all naturals 
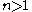. As per the above remarks, we easily see that for all rationals, 
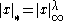, thus demonstrating equivalence to the real absolute value.
Case II:
As this valuation is non-trivial, there must be a natural number for which 
. Factorising this natural,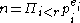 
yields 
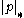must be less than 1, for at least one of the prime
factors
. We claim than in fact, that this is so for only one.
Suppose per contra that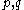
are distinct primes with absolute value less than 1. First, let 
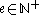be such that 
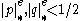. By the Euclidean algorithm, let 
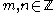be integers for which 
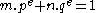. This yields 
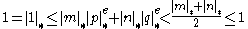, a contradiction.
So must have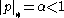
for some prime, and 
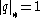all other primes. Letting 
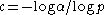, we see that for general positive naturals 
; 
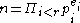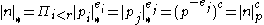. As per the above remarks we see that 
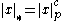all rationals, implying the absolute value is equivalent to the 
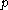-adic one.
One can also show a stronger conclusion, namely that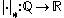
is a nontrivial absolute value if and only if either 
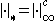for some 
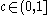or 
for some 
.
Alexander Ostrowski
Alexander Markowich Ostrowski , was a mathematician.His father Mark having been a merchant, Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university...
(1916), states that any non-trivial absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
on the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q is equivalent to either the usual real absolute value or a p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
absolute value.
Definitions
Two absolute valueAbsolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
s
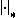and on a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
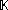are defined to be equivalent if there exists a real number c > 0 such that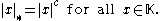Observe that this is stronger than saying that the two absolute-value structures are topologically isomorphic.
The trivial absolute value on any field
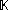is defined to be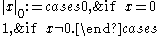The real absolute value on the rationals
is the normal absolute value on the reals, defined to be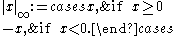This is sometimes written with a subscript 1 instead of infinity.
For a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, the p-adic absolute value on
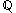is defined as follows: any non-zero rational x, can be written uniquely as 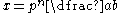with a, b and p pairwise coprimePairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
and
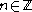some integer; so we define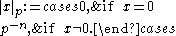Proof
Consider a non-trivial absolute value on the rationals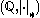. We consider two cases, (i) 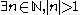and (ii) 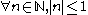. It suffices for us to consider the valuation of integers greater than one. For if we find some 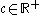for which 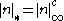for all naturals greater than one; then this relation trivially holds for 0 and 1, and for positive rationals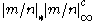;and for negative rationals
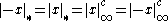. Case I: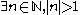 
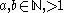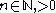Consider the following calculation. Let . Let . Expressing in baseRadix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
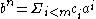yields , where each 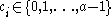and .Then we see, by the properties of an absolute value:
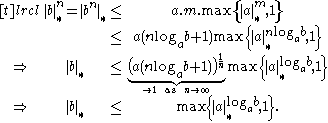
Now choose
such that 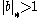.Using this in the above ensures that 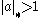regardless of the choice of (else 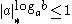implying 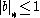). Thus for any choice of above, we get 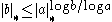, i.e. 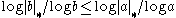.By symmetry, this inequality is an equality.
Since
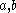were arbitrary, there is a constant, for which 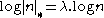,i.e.
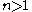for all naturals . As per the above remarks, we easily see that for all rationals, 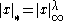, thus demonstrating equivalence to the real absolute value. Case II: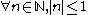 
As this valuation is non-trivial, there must be a natural number for which . Factorising this natural, 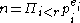yields 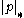must be less than 1, for at least one of the primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
factors
. We claim than in fact, that this is so for only one.Suppose per contra that
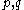are distinct primes with absolute value less than 1. First, let 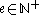be such that 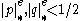. By the Euclidean algorithm, let 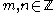be integers for which 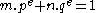. This yields 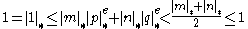, a contradiction.So must have
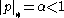for some prime, and 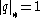all other primes. Letting 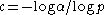, we see that for general positive naturals 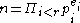; 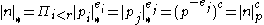. As per the above remarks we see that 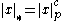all rationals, implying the absolute value is equivalent to the 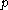-adic one.One can also show a stronger conclusion, namely that
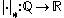is a nontrivial absolute value if and only if either 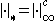for some 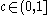or for some .