
L-reduction
Encyclopedia
In computer science
, in particular in the study of approximation algorithms, an
L-reduction ("linear reduction") is a transformation of optimization problem
s which linearly preserves approximability features. L-reductions in studies of approximability of optimization problem
s play a similar role to that of polynomial reductions
in the studies of computational complexity
of decision problem
s.
The term L reduction is sometimes used to refer to log-space reduction
s, by analogy with the complexity class L
, but this is a different concept.
s and cA and cB their respective cost functions. A pair of functions f and g is an L-reduction if all of the following conditions are met:
f for a problem A be such that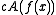 is at most
is at most 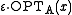 away from
away from 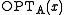 , for every instance x. (In this notation, + implicitly means a minimization problem, and
, for every instance x. (In this notation, + implicitly means a minimization problem, and 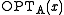 means a maximization problem.)
means a maximization problem.)
The main point of an L-reduction is the following: given a (f,g,α,β) L-reduction from problem A to problem B, and a (1±ε)-approximation algorithm
for B, we obtain a polynomial-time (1±δ)-approximation algorithm
for A where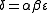 .
.
This implies that if B has a polynomial-time approximation scheme
then so does A.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, in particular in the study of approximation algorithms, an
L-reduction ("linear reduction") is a transformation of optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s which linearly preserves approximability features. L-reductions in studies of approximability of optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s play a similar role to that of polynomial reductions
Polynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
in the studies of computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s.
The term L reduction is sometimes used to refer to log-space reduction
Log-space reduction
In computational complexity theory, a log-space reduction is a reduction computable by a deterministic Turing machine using logarithmic space. Conceptually, this means it can keep a constant number of pointers into the input, along with a logarithmic number of fixed-size integers...
s, by analogy with the complexity class L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
, but this is a different concept.
Definition
Let A and B be optimization problemOptimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s and cA and cB their respective cost functions. A pair of functions f and g is an L-reduction if all of the following conditions are met:
- functions f and g are computable in polynomial time,
- if x is an instance of problem A, then f(x) is an instance of problem B,
- if y is a solution to f(x), then g(y) is a solution to x,
- there exists a positive constant α such that
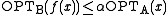 ,
, - there exists a positive constant β such that for every solution y to f(x)
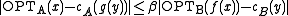 .
.
Properties
Let a (1±ε)-approximation algorithmApproximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
f for a problem A be such that
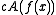 is at most
is at most 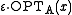 away from
away from 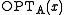 , for every instance x. (In this notation, + implicitly means a minimization problem, and
, for every instance x. (In this notation, + implicitly means a minimization problem, and 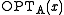 means a maximization problem.)
means a maximization problem.)The main point of an L-reduction is the following: given a (f,g,α,β) L-reduction from problem A to problem B, and a (1±ε)-approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for B, we obtain a polynomial-time (1±δ)-approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for A where
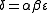 .
.This implies that if B has a polynomial-time approximation scheme
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
then so does A.
See also
- MAXSNP
- PTAS reductionPTAS reductionIn computational complexity theory, a PTAS reduction is a reduction that is often used to perform reductions between solutions to optimization problems. It preserves the property that a problem has a polynomial time approximation scheme and is used to define completeness for certain classes of...
- Dominating set#L-reductions: an example with α = β = 1

