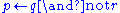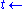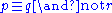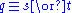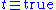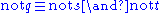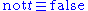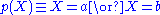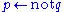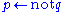Negation as failure
Encyclopedia
Negation as failure is a non-monotonic
inference rule in logic programming
, used to derive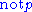 (i.e. that
(i.e. that 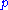 is assumed not to hold) from failure to derive
is assumed not to hold) from failure to derive 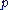 . Note that
. Note that 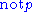 can be different from the statement
can be different from the statement 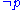 of the logical negation
of the logical negation
of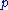 , depending on the completeness of the inference algorithm and thus also on the formal logic system.
, depending on the completeness of the inference algorithm and thus also on the formal logic system.
Negation as failure has been an important feature of logic programming since the earliest days of both Planner and Prolog
. In Prolog, it is usually implemented using Prolog's extralogical constructs.
which says that if the goal to prove p fails, then assert ¬p. Note that the above example uses true mathematical negation, which cannot be expressed in Prolog.
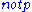 can occur in the body of clauses and can be used to derive other NAF literals. For example, given only the four clauses
can occur in the body of clauses and can be used to derive other NAF literals. For example, given only the four clauses
NAF derives ,
, 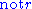 and
and 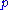 .
.
 are interpreted as "if and only if", written as "iff" or "
are interpreted as "if and only if", written as "iff" or " ".
".
For example, the completion of the four clauses above is
The NAF inference rule simulates reasoning explicitly with the completion, where both sides of the equivalence are negated and negation on the right-hand side is distributed down to atomic formula
e. For example, to show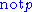 , NAF simulates reasoning with the equivalences
, NAF simulates reasoning with the equivalences
In the non-propositional case, the completion needs to be augmented with equality axioms, to formalise the assumption that individuals with distinct names are distinct. NAF simulates this by failure of unification. For example, given only the two clauses
NAF derives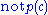 .
.
The completion of the program is
augmented with unique names axioms and domain closure axioms.
The completion semantics is closely related both to circumscription and to the closed world assumption
.
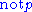 of a NAF inference as the classical negation
of a NAF inference as the classical negation 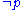 of
of 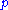 . However, Michael Gelfond [1987] showed that it is also possible to interpret
. However, Michael Gelfond [1987] showed that it is also possible to interpret 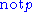 literally as "
literally as "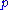 can not be shown", "
can not be shown", "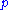 is not known" or "
is not known" or "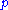 is not believed", as in autoepistemic logic
is not believed", as in autoepistemic logic
. The autoepistemic interpretation was developed further by Gelfond and Lifschitz [1988] and is the basis of answer set programming
.
The autoepistemics semantics of a pure Prolog program P with NAF literals is obtained by "expanding" P with a set of ground (variable-free) NAF literals Δ that is stable
in the sense that
In other words, a set of assumptions Δ about what can not be shown is stable
if and only if Δ is the set of all sentences that truly can not be shown from the program P expanded by Δ. Here, because of the simple syntax of pure Prolog programs, "implied by" can be understood very simply as derivability using modus ponens and universal instantiation alone.
A program can have zero, one or more stable expansions. For example
has no stable expansions.
has exactly one stable expansion Δ = {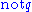 }
}
has exactly two stable expansions Δ1 = { } and Δ2 = {
} and Δ2 = {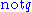 }.
}.
The autoepistemic interpretation of NAF can be combined with classical negation, as in extended logic programming and answer set programming
. Combining the two negations, it is possible to express, for example
Non-monotonic logic
A non-monotonic logic is a formal logic whose consequence relation is not monotonic. Most studied formal logics have a monotonic consequence relation, meaning that adding a formula to a theory never produces a reduction of its set of consequences. Intuitively, monotonicity indicates that learning a...
inference rule in logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
, used to derive
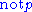 (i.e. that
(i.e. that 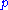 is assumed not to hold) from failure to derive
is assumed not to hold) from failure to derive 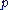 . Note that
. Note that 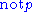 can be different from the statement
can be different from the statement 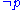 of the logical negation
of the logical negationNegation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
of
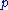 , depending on the completeness of the inference algorithm and thus also on the formal logic system.
, depending on the completeness of the inference algorithm and thus also on the formal logic system.Negation as failure has been an important feature of logic programming since the earliest days of both Planner and Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
. In Prolog, it is usually implemented using Prolog's extralogical constructs.
Planner semantics
In Planner, negation as failure could be implemented as follows:- if (not (goal p)), then (assert ¬p)
which says that if the goal to prove p fails, then assert ¬p. Note that the above example uses true mathematical negation, which cannot be expressed in Prolog.
Prolog semantics
In pure Prolog, NAF literals of the form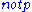 can occur in the body of clauses and can be used to derive other NAF literals. For example, given only the four clauses
can occur in the body of clauses and can be used to derive other NAF literals. For example, given only the four clausesNAF derives
 ,
, 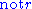 and
and 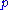 .
.Completion semantics
The semantics of NAF remained an open issue until Keith Clark [1978] showed that it is correct with respect to the completion of the logic program, where, loosely speaking, "only" and are interpreted as "if and only if", written as "iff" or "
are interpreted as "if and only if", written as "iff" or " ".
".For example, the completion of the four clauses above is
The NAF inference rule simulates reasoning explicitly with the completion, where both sides of the equivalence are negated and negation on the right-hand side is distributed down to atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e. For example, to show
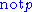 , NAF simulates reasoning with the equivalences
, NAF simulates reasoning with the equivalencesIn the non-propositional case, the completion needs to be augmented with equality axioms, to formalise the assumption that individuals with distinct names are distinct. NAF simulates this by failure of unification. For example, given only the two clauses
-
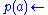
-
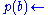 t
t
NAF derives
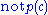 .
.The completion of the program is
augmented with unique names axioms and domain closure axioms.
The completion semantics is closely related both to circumscription and to the closed world assumption
Closed world assumption
The closed world assumption is the presumption that what is not currently known to be true, is false. The same name also refers to a logical formalization of this assumption by Raymond Reiter. The opposite of the closed world assumption is the open world assumption , stating that lack of knowledge...
.
Autoepistemic semantics
The completion semantics justifies interpreting the result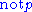 of a NAF inference as the classical negation
of a NAF inference as the classical negation 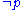 of
of 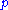 . However, Michael Gelfond [1987] showed that it is also possible to interpret
. However, Michael Gelfond [1987] showed that it is also possible to interpret 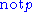 literally as "
literally as "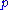 can not be shown", "
can not be shown", "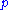 is not known" or "
is not known" or "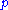 is not believed", as in autoepistemic logic
is not believed", as in autoepistemic logicAutoepistemic logic
The autoepistemic logic is a formal logic for the representation and reasoning of knowledge about knowledge. While propositional logic can only express facts, autoepistemic logic can express knowledge and lack of knowledge about facts....
. The autoepistemic interpretation was developed further by Gelfond and Lifschitz [1988] and is the basis of answer set programming
Answer set programming
Answer set programming is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers -- programs for generating stable...
.
The autoepistemics semantics of a pure Prolog program P with NAF literals is obtained by "expanding" P with a set of ground (variable-free) NAF literals Δ that is stable
Stable model semantics
The concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program completion and the well-founded semantics...
in the sense that
- Δ = {
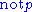 |
| 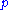 is not implied by P ∪ Δ}
is not implied by P ∪ Δ}
In other words, a set of assumptions Δ about what can not be shown is stable
Stable model semantics
The concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program completion and the well-founded semantics...
if and only if Δ is the set of all sentences that truly can not be shown from the program P expanded by Δ. Here, because of the simple syntax of pure Prolog programs, "implied by" can be understood very simply as derivability using modus ponens and universal instantiation alone.
A program can have zero, one or more stable expansions. For example
has no stable expansions.
has exactly one stable expansion Δ = {
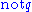 }
}has exactly two stable expansions Δ1 = {
 } and Δ2 = {
} and Δ2 = {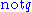 }.
}.The autoepistemic interpretation of NAF can be combined with classical negation, as in extended logic programming and answer set programming
Answer set programming
Answer set programming is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers -- programs for generating stable...
. Combining the two negations, it is possible to express, for example
-
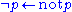 (the closed world assumption) and
(the closed world assumption) and -
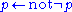 (
(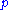 holds by default).
holds by default).
External links
- Report from the W3C Workshop on Rule Languages for Interoperability. Includes notes on NAF and SNAF (scoped negation as failure).