Autoepistemic logic
Encyclopedia
The autoepistemic logic is a formal logic
for the representation and reasoning of knowledge about knowledge. While propositional logic can only express facts, autoepistemic logic can express knowledge and lack of knowledge about facts.
The stable model semantics
, which is used to give a semantics to logic programming
with negation as failure, can be seen as a simplified form of autoepistemic logic.
of autoepistemic logic extends that of propositional logic by a modal operator
indicating knowledge: if 
is a formula,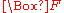 
indicates that 
is known. As a result, 
indicates that 
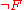is known and 
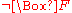indicates that 
is not known.
This syntax is used for allowing reasoning based on knowledge of facts. For example,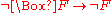
means that 
is assumed false if it is not known to be true. This is a form of negation as failure.
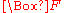are true and which ones are false. In particular, the expansions of an autoepistemic formula 
makes this distinction for every subformula 
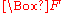contained in 
. This distinction allows 
to be treated as a propositional formula
, as all its subformulae containing
are either true or false. In particular, checking whether 
entails 
in this condition can be done using the rules of the propositional calculus. In order for an initial assumption to be an expansion, it must be that a subformula 
is entailed if and only if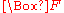 
has been initially assumed true.
For example, in the formula
, there is only a single “boxed subformula”, which is 
. Therefore, there are only two candidate expansions, assuming it true or false, respectively. The check for them being actual expansions is as follows.
is false : with this assumption, 
becomes tautological, as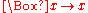 
is equivalent to 
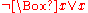, and 
is assumed true; therefore, 
is not entailed. This result confirms the assumption implicit in 
being false, that is, that 
is not currently known. Therefore, the assumption that 
is false is an expansion.
is true : together with this assumption, 
entails 
; therefore, the initial assumption that is implicit in 
being true, i.e., that 
is known to be true, is satisfied. As a result, this is another expansion.
The formula
has therefore two expansions, one in which 
is not known and one in which 
is known. The second one has been regarded as unintuitive, as the initial assumption that 
is true is the only reason why 
is true, which confirms the assumption. In other words, this is a self-supporting assumption. A logic allowing such a self-support of beliefs is called not strongly grounded to differentiate them from strongly grounded logics, in which self-support is not possible. Strongly grounded variants of autoepistemic logic exist.
, the known/unknown duality of truth values is replaced by a degree of certainty of a fact or deduction; certainty may vary from 0 (completely uncertain/unknown) to 1 (certain/known). In probabilistic logic network
s, truth values are also given a probabilistic interpretation (i.e. truth values may be uncertain, and, even if almost certain, they may still be "probably" true (or false).)
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
for the representation and reasoning of knowledge about knowledge. While propositional logic can only express facts, autoepistemic logic can express knowledge and lack of knowledge about facts.
The stable model semantics
Stable model semantics
The concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program completion and the well-founded semantics...
, which is used to give a semantics to logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
with negation as failure, can be seen as a simplified form of autoepistemic logic.
Syntax
The syntaxSyntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
of autoepistemic logic extends that of propositional logic by a modal operator
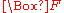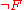indicating knowledge: if is a formula, indicates that is known. As a result, indicates that is known and 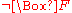indicates that is not known.This syntax is used for allowing reasoning based on knowledge of facts. For example,
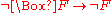means that is assumed false if it is not known to be true. This is a form of negation as failure.Semantics
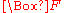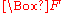The semantics of autoepistemic logic is based on the expansions of a theory, which have a role similar to models in propositional logic. While a propositional model specifies which atoms are true or false, an expansion specifies which formulae are true and which ones are false. In particular, the expansions of an autoepistemic formula makes this distinction for every subformula contained in . This distinction allows to be treated as a propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
, as all its subformulae containing
are either true or false. In particular, checking whether entails in this condition can be done using the rules of the propositional calculus. In order for an initial assumption to be an expansion, it must be that a subformula is entailed if and only if 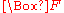has been initially assumed true.For example, in the formula
, there is only a single “boxed subformula”, which is . Therefore, there are only two candidate expansions, assuming it true or false, respectively. The check for them being actual expansions is as follows. is false : with this assumption, becomes tautological, as 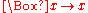is equivalent to 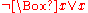, and is assumed true; therefore, is not entailed. This result confirms the assumption implicit in being false, that is, that is not currently known. Therefore, the assumption that is false is an expansion. is true : together with this assumption, entails ; therefore, the initial assumption that is implicit in being true, i.e., that is known to be true, is satisfied. As a result, this is another expansion.The formula
has therefore two expansions, one in which is not known and one in which is known. The second one has been regarded as unintuitive, as the initial assumption that is true is the only reason why is true, which confirms the assumption. In other words, this is a self-supporting assumption. A logic allowing such a self-support of beliefs is called not strongly grounded to differentiate them from strongly grounded logics, in which self-support is not possible. Strongly grounded variants of autoepistemic logic exist.Generalizations
In uncertain inferenceUncertain inference
Uncertain inference was first described by Rijsbergen as a way to formally define a query and document relationship in Information retrieval. This formalization is a logical implication with an attached measure of uncertainty.-Definitions:...
, the known/unknown duality of truth values is replaced by a degree of certainty of a fact or deduction; certainty may vary from 0 (completely uncertain/unknown) to 1 (certain/known). In probabilistic logic network
Probabilistic logic network
A probabilistic logic network is a novel conceptual, mathematical and computational approach to uncertain inference; inspired by logic programming, but using probabilities in place of crisp truth values, and fractional uncertainty in place of crisp known/unknown values...
s, truth values are also given a probabilistic interpretation (i.e. truth values may be uncertain, and, even if almost certain, they may still be "probably" true (or false).)