Closed world assumption
Encyclopedia
The closed world assumption
(CWA) is the presumption that what is not currently known to be true, is false. The same name also refers to a logical
formalization of this assumption by Raymond Reiter
. The opposite of the closed world assumption is the open world assumption (OWA)
, stating that lack of knowledge does not imply falsity. Decisions on CWA vs.OWA determine the understanding of the actual semantics of a conceptual expression with the same notations of concepts. A successful formalization of natural language semantics usually can not avoid an explicit revelation of the implicit logical backgrounds based on whether CWA or OWA.
Negation as failure is related to the closed world assumption, as it amounts to believing false every predicate that cannot be proved to be true.
In the knowledge management
arena, the closed world assumption is used in at least two situations: 1) when the knowledge base is known to be complete (e.g., a corporate database containing records for every employee), and 2) when the knowledge base is known to be incomplete but a "best" definite answer must be derived from incomplete information. For example, if a database
contains the following table reporting editors who have worked on a given article, a query on the people not having edited the article on Formal Logic is usually expected to return “Sarah Johnson”.
In the closed world assumption, the table is assumed to be complete (it lists all editor-article relationships), and Sarah Johnson is the only editor who has not edited the article on Formal Logic. In contrast, with the open world assumption the table is not assumed to contain all editor-article tuples, and the answer to who has not edited the Formal Logic article is unknown. There is an unknown number of editors not listed in the table, and an unknown number of articles edited by Sarah Johnson that are also not listed in the table.
consists in adding to the knowledge base the negation of the literals that are not currently entailed by it. The result of this addition is always consistent if the knowledge base is in Horn form
, but is not guaranteed to be consistent otherwise. For example, the knowledge base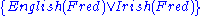
entails neither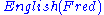
nor 
.
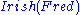Adding the negation of these two literals to the knowledge base leads to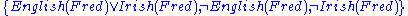
which is inconsistent. In other words, this formalization of the closed world assumption sometimes turns a consistent knowledge base into an inconsistent one. The closed world assumption does not introduce an inconsistency on a knowledge base
exactly when the intersection of all Herbrand models of 
is also a model of 
; in the propositional case, this condition is equivalent to 
having a single minimal model, where a model is minimal if no other models has a subset of variables assigned to true.
Alternative formalizations not suffering from this problem have been proposed. In the following description, the considered knowledge base
is assumed to be propositional. In all cases, the formalization of the closed world assumption is based on adding to 
the negation of the formulae that are “free for negation” for 
, i.e., the formulae that can be assumed to be false. In other words, the closed world assumption applied to a propositional formula
generates the formula: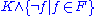
.
The set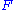
of formulae that are free for negation in 
can be defined in different ways, leading to different formalizations of the closed world assumption. The following are the definitions of 
being free for negation in the various formalizations.
CWA (closed world assumption) :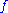
is a positive literal not entailed by 
;
GCWA (generalized CWA) :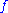
is a positive literal such that, for every positive clause 
such that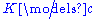 
, it holds 
;
EGCWA (extended GCWA): same as above, but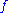
is a conjunction of positive literals;
CCWA (careful CWA): same as GCWA, but a positive clause is only considered if it is composed of positive literals of a given set and (both positive and negative) literals from another set;
ECWA (extended CWA): similar to CCWA, but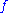
is an arbitrary formula not containing literals from a given set.
The ECWA and the formalism of circumscription coincide on propositional theories. The complexity of query answering (checking whether a formula is entailed by another one under the closed world assumption) is typically in the second level of the polynomial hierarchy
for general formulae, and ranges from P
to coNP for Horn formulae
. Checking whether the original closed world assumption introduces an inconsistency requires at most a logarithmic number of calls to an NP oracle
; however, the exact complexity of this problem is not currently known.
Closed world assumption
The closed world assumption is the presumption that what is not currently known to be true, is false. The same name also refers to a logical formalization of this assumption by Raymond Reiter. The opposite of the closed world assumption is the open world assumption , stating that lack of knowledge...
(CWA) is the presumption that what is not currently known to be true, is false. The same name also refers to a logical
Formal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
formalization of this assumption by Raymond Reiter
Raymond Reiter
Raymond Reiter , was a Canadian computer scientist and logician. He was one of the founders of the field of non-monotonic reasoning with his work on default logic, model-based diagnosis, closed world reasoning, and truth maintenance systems...
. The opposite of the closed world assumption is the open world assumption (OWA)
Open World Assumption
In formal logic, the open world assumption is the assumption that the truth-value of a statement is independent of whether or not it is known by any single observer or agent to be true. It is the opposite of the closed world assumption, which holds that any statement that is not known to be true is...
, stating that lack of knowledge does not imply falsity. Decisions on CWA vs.OWA determine the understanding of the actual semantics of a conceptual expression with the same notations of concepts. A successful formalization of natural language semantics usually can not avoid an explicit revelation of the implicit logical backgrounds based on whether CWA or OWA.
Negation as failure is related to the closed world assumption, as it amounts to believing false every predicate that cannot be proved to be true.
In the knowledge management
Knowledge management
Knowledge management comprises a range of strategies and practices used in an organization to identify, create, represent, distribute, and enable adoption of insights and experiences...
arena, the closed world assumption is used in at least two situations: 1) when the knowledge base is known to be complete (e.g., a corporate database containing records for every employee), and 2) when the knowledge base is known to be incomplete but a "best" definite answer must be derived from incomplete information. For example, if a database
Database
A database is an organized collection of data for one or more purposes, usually in digital form. The data are typically organized to model relevant aspects of reality , in a way that supports processes requiring this information...
contains the following table reporting editors who have worked on a given article, a query on the people not having edited the article on Formal Logic is usually expected to return “Sarah Johnson”.
| Edit | |
|---|---|
| Editor | Article |
| John Doe | Formal Logic |
| John Doe | Closed World Assumption |
| Joshua A. Norton | Formal Logic |
| Sarah Johnson | Introduction to Spatial Databases |
| Charles Ponzi | Formal Logic |
| Emma Lee-Choon | Formal Logic |
In the closed world assumption, the table is assumed to be complete (it lists all editor-article relationships), and Sarah Johnson is the only editor who has not edited the article on Formal Logic. In contrast, with the open world assumption the table is not assumed to contain all editor-article tuples, and the answer to who has not edited the Formal Logic article is unknown. There is an unknown number of editors not listed in the table, and an unknown number of articles edited by Sarah Johnson that are also not listed in the table.
Formalization in logic
The first formalization of the closed world assumption in formal logicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
consists in adding to the knowledge base the negation of the literals that are not currently entailed by it. The result of this addition is always consistent if the knowledge base is in Horn form
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
, but is not guaranteed to be consistent otherwise. For example, the knowledge base
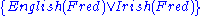
entails neither
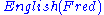nor 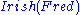.Adding the negation of these two literals to the knowledge base leads to
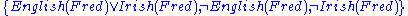
which is inconsistent. In other words, this formalization of the closed world assumption sometimes turns a consistent knowledge base into an inconsistent one. The closed world assumption does not introduce an inconsistency on a knowledge base
exactly when the intersection of all Herbrand models of is also a model of ; in the propositional case, this condition is equivalent to having a single minimal model, where a model is minimal if no other models has a subset of variables assigned to true.Alternative formalizations not suffering from this problem have been proposed. In the following description, the considered knowledge base
is assumed to be propositional. In all cases, the formalization of the closed world assumption is based on adding to the negation of the formulae that are “free for negation” for , i.e., the formulae that can be assumed to be false. In other words, the closed world assumption applied to a propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
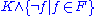generates the formula:.The set
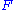of formulae that are free for negation in can be defined in different ways, leading to different formalizations of the closed world assumption. The following are the definitions of being free for negation in the various formalizations.CWA (closed world assumption) :
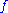is a positive literal not entailed by ;GCWA (generalized CWA) :
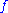is a positive literal such that, for every positive clause such that 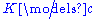, it holds ;EGCWA (extended GCWA): same as above, but
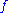is a conjunction of positive literals;CCWA (careful CWA): same as GCWA, but a positive clause is only considered if it is composed of positive literals of a given set and (both positive and negative) literals from another set;
ECWA (extended CWA): similar to CCWA, but
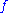is an arbitrary formula not containing literals from a given set.The ECWA and the formalism of circumscription coincide on propositional theories. The complexity of query answering (checking whether a formula is entailed by another one under the closed world assumption) is typically in the second level of the polynomial hierarchy
Polynomial hierarchy
In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines...
for general formulae, and ranges from P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
to coNP for Horn formulae
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
. Checking whether the original closed world assumption introduces an inconsistency requires at most a logarithmic number of calls to an NP oracle
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
; however, the exact complexity of this problem is not currently known.
See also
- Open world assumptionOpen World AssumptionIn formal logic, the open world assumption is the assumption that the truth-value of a statement is independent of whether or not it is known by any single observer or agent to be true. It is the opposite of the closed world assumption, which holds that any statement that is not known to be true is...
- Non-monotonic logicNon-monotonic logicA non-monotonic logic is a formal logic whose consequence relation is not monotonic. Most studied formal logics have a monotonic consequence relation, meaning that adding a formula to a theory never produces a reduction of its set of consequences. Intuitively, monotonicity indicates that learning a...
- Circumscription (logic)
- Negation as failure
- Default logicDefault logicDefault logic is a non-monotonic logic proposed by Raymond Reiter to formalize reasoning with default assumptions.Default logic can express facts like “by default, something is true”; by contrast, standard logic can only express that something is true or that something is false...
- Stable model semanticsStable model semanticsThe concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program completion and the well-founded semantics...
- Unique name assumptionUnique name assumptionThe Unique Name Assumption is a concept from ontology languages and description logics. In logics with the unique name assumption, different names always refer to different entities in the world...
External links
- http://www.betaversion.org/~stefano/linotype/news/91/
- Closed World Reasoning in the Semantic Web through Epistemic Operators
- Excerpt from Reiter's 1978 talk on the closed world assumption