
Mycielskian
Encyclopedia
In the mathematical
area of graph theory
, the Mycielskian or Mycielski graph of an undirected graph G is a graph μ(G) formed from G by a construction of , who used it to show that there exist triangle-free graph
s with arbitrarily large chromatic number.
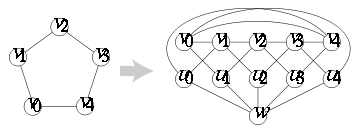 Let the n vertices of the given graph G be v0, v1, etc. The Mycielski graph of G contains G itself as an isomorphic subgraph, together with n+1 additional vertices: a vertex ui corresponding to each vertex vi of G, and another vertex w. Each vertex ui is connected by an edge to w, so that these vertices form a subgraph in the form of a star K1,n. In addition, for each edge vivj of G, the Mycielski graph includes two edges, uivj and viuj.
Let the n vertices of the given graph G be v0, v1, etc. The Mycielski graph of G contains G itself as an isomorphic subgraph, together with n+1 additional vertices: a vertex ui corresponding to each vertex vi of G, and another vertex w. Each vertex ui is connected by an edge to w, so that these vertices form a subgraph in the form of a star K1,n. In addition, for each edge vivj of G, the Mycielski graph includes two edges, uivj and viuj.
Thus, if G has n vertices and m edges, μ(G) has 2n+1 vertices and 3m+n edges.
with vertices vi for 0 ≤ i ≤ 4.
The resulting Mycielskian is the Grötzsch graph
, an 11-vertex graph with 20 edges. The Grötzsch graph is the smallest triangle-free 4-chromatic graph .
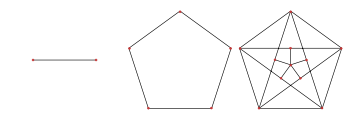 Applying the Mycielskian repeatedly, starting with a graph with a single edge, produces a sequence of graphs Mi = μ(Mi-1), also sometimes called the Mycielski graphs. The first few graphs in this sequence are the graph M2 = K2 with two vertices connected by an edge, the cycle graph
Applying the Mycielskian repeatedly, starting with a graph with a single edge, produces a sequence of graphs Mi = μ(Mi-1), also sometimes called the Mycielski graphs. The first few graphs in this sequence are the graph M2 = K2 with two vertices connected by an edge, the cycle graph
M3 = C5, and the Grötzsch graph
with 11 vertices and 20 edges.
In general, the graphs Mi in this sequence are triangle-free
, (i-1)-vertex-connected
, and i-chromatic. Mi has 3 × 2i-2 - 1 vertices . The numbers of edges in Mi, for small i, are

G × H, where H is a path of length i with a self-loop at one end, and then collapsing into a single supervertex all of the vertices associated with the vertex of H at the other end of the path from the self-loop. The Mycielskian itself can be formed in this way as Δ2(G).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Mycielskian or Mycielski graph of an undirected graph G is a graph μ(G) formed from G by a construction of , who used it to show that there exist triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
s with arbitrarily large chromatic number.
Construction

Thus, if G has n vertices and m edges, μ(G) has 2n+1 vertices and 3m+n edges.
Example
The illustration shows Mycielski's construction as applied to a 5-vertex cycle graphCycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
with vertices vi for 0 ≤ i ≤ 4.
The resulting Mycielskian is the Grötzsch graph
Grötzsch graph
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem ...
, an 11-vertex graph with 20 edges. The Grötzsch graph is the smallest triangle-free 4-chromatic graph .
Iterated Mycielskians

Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
M3 = C5, and the Grötzsch graph
Grötzsch graph
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem ...
with 11 vertices and 20 edges.
In general, the graphs Mi in this sequence are triangle-free
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
, (i-1)-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
, and i-chromatic. Mi has 3 × 2i-2 - 1 vertices . The numbers of edges in Mi, for small i, are
- 0, 0, 1, 5, 20, 71, 236, 755, 2360, 7271, 22196, 67355, ... .
Properties

- If G has chromatic number k, then μ(G) has chromatic number k + 1 .
- If G is triangle-freeTriangle-free graphIn the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
, then so is μ(G) . - If G is a factor-critical graphFactor-critical graphIn graph theory, a mathematical discipline, a factor-critical graph is a graph with vertices in which every subgraph of vertices has a perfect matching, a subset of its edges such that each of the vertices is the endpoint of exactly one of the edges in the subset.A matching that covers all but...
, then so is μ(G) . In particular, every graph Mi for i ≥ 2 is factor-critical. - If G has a Hamiltonian cycle, then so does μ(G) .
Cones over graphs
A generalization of the Mycielskian, called a cone over a graph, was introduced by and further studied by and . In this construction, one forms a graph Δi(G) from a given graph G by taking the tensor product of graphsTensor product of graphs
In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and...
G × H, where H is a path of length i with a self-loop at one end, and then collapsing into a single supervertex all of the vertices associated with the vertex of H at the other end of the path from the self-loop. The Mycielskian itself can be formed in this way as Δ2(G).

