
Morse-Palais lemma
Encyclopedia
In mathematics
, the Morse–Palais lemma is a result in the calculus of variations
and theory of Hilbert spaces. Roughly speaking, it states that a smooth
enough function
near a critical point can be expressed as a quadratic form
after a suitable change of coordinates.
The Morse–Palais lemma was originally proved in the finite-dimensional case by the American
mathematician
Marston Morse
, using the Gram–Schmidt orthogonalization process
. This result plays a crucial role in Morse theory
. The generalization to Hilbert spaces is due to Richard Palais.
Hilbert space, and let U be an open neighbourhood
of 0 in H. Let f : U → R be a (k + 2)-times continuously differentiable function
with k ≥ 1, i.e. f ∈ Ck+2(U; R). Assume that f(0) = 0 and that 0 is a non-degenerate critical point
of f, i.e. the second derivative D2f(0) defines an isomorphism
of H with its continuous dual space H∗ by
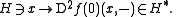
Then there exists a subneighbourhood V of 0 in U, a diffeomorphism
φ : V → V that is Ck with Ck inverse, and an invertible symmetric operator A : H → H, such that

for all x ∈ V.
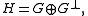
such that, if one writes
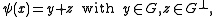
then
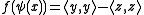
for all x ∈ V.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Morse–Palais lemma is a result in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
and theory of Hilbert spaces. Roughly speaking, it states that a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
enough function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
near a critical point can be expressed as a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
after a suitable change of coordinates.
The Morse–Palais lemma was originally proved in the finite-dimensional case by the American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
, using the Gram–Schmidt orthogonalization process
Gram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
. This result plays a crucial role in Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. The generalization to Hilbert spaces is due to Richard Palais.
Statement of the lemma
Let (H, 〈 , 〉) be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
Hilbert space, and let U be an open neighbourhood
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of 0 in H. Let f : U → R be a (k + 2)-times continuously differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
with k ≥ 1, i.e. f ∈ Ck+2(U; R). Assume that f(0) = 0 and that 0 is a non-degenerate critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of f, i.e. the second derivative D2f(0) defines an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of H with its continuous dual space H∗ by
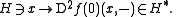
Then there exists a subneighbourhood V of 0 in U, a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
φ : V → V that is Ck with Ck inverse, and an invertible symmetric operator A : H → H, such that

for all x ∈ V.
Corollary
Let f : U → R be Ck+2 such that 0 is a non-degenerate critical point. Then there exists a Ck-with-Ck-inverse diffeomorphism ψ : V → V and an orthogonal decomposition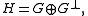
such that, if one writes
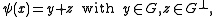
then
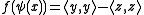
for all x ∈ V.

