
Modularity (networks)
Encyclopedia
Modularity is one measure of the structure of networks
or graphs
. It measures the strength of division of a network into modules (also called groups, clusters or communities). Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. Modularity is often used in optimisation methods for detecting community structure
in networks.
There are different methods for calculating modularity. In the most common version of the concept, the randomization of the edges is done so as to preserve the degree
of each vertex. Let us consider a graph with nodes
nodes
and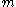 links (edges) such that the graph can be partitioned into 2 communities using a membership variable
links (edges) such that the graph can be partitioned into 2 communities using a membership variable  . If a node
. If a node 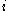 belongs to community 1,
belongs to community 1, 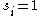 , or if
, or if 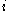 belongs to community 2,
belongs to community 2, 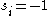 . Let the adjacency matrix
. Let the adjacency matrix
for the network be represented by , where
, where 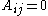 means there's no edge (no interaction) between nodes
means there's no edge (no interaction) between nodes 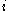 and
and 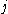 and
and 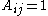 means there is an edge between the two. Also for simplicity we consider an undirected network. Thus
means there is an edge between the two. Also for simplicity we consider an undirected network. Thus 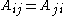 . (It is important to note that multiple edges may exist between 2 nodes and here we assess the simplest case).
. (It is important to note that multiple edges may exist between 2 nodes and here we assess the simplest case).
Modularity Q is then defined as the fraction of edges that fall within group 1 or 2, minus the expected number of edges within group 1 and 2 for a random graph with same node degree distribution as the given network.
The expected number of edges shall be computed using the concept of Configuration Models . The configuration model is a randomized realization of a particular network. Given a network with n nodes, where each node i has a node degree ki, the configuration model cuts each edge into 2 halves, and then each half edge, called a stub, is rewired randomly with any other stub in the network even allowing self loops. Thus, even though the node degree distribution of the graph remains intact, the configuration model results in a completely random network.
Let the total number of stubs be ln
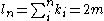
Now, if we randomly select two nodes i and j with node degrees ki and kj respectively and rewire the stubsfor these 2 nodes, then,
Expected [Full edges between i and j] = (Full edges between i and j)/(Total number of rewirings possible) (2)
Total number of rewritings possible = number of stubs remaining after choosing a particular stub
= ln-1= l n for large n
Thus, Expected [Number of full edges between i and j]=(ki* kj)/ln =(ki kj)/2m.
Hence, the actual number of edges between i and j minus expected number of edges between them is Aij-(ki kj )/2m. Thus using
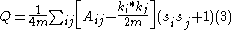
It is important to note that (3) holds good for partitioning into 2 communities only. Hierarchical partitioning (i.e. partitioning into 2 communities, then the 2 sub-communities further partitioned into 2 smaller sub communities only to maximize Q) is a possible approach to identify multiple communities in a network. Additionally, (3) can be generalized for partitioning a network into c communities. .
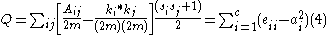
where eii is the fraction of edges with both end vertices in the same community i.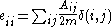
and ai is the fraction of edges with at least one end vertex in community i.
The communities in the graph are represented by the red, green and blue node clusters in Fig 1. The optimal community partitions are depicted in Fig 2.
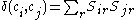
and hence
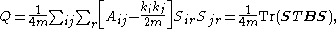
where S is the (non-square) matrix having elements Sir and B is the so-called modularity matrix, which has elements
All rows and columns of the modularity matrix sum to zero, which means that the modularity of an undivided network is also always zero.
For networks divided into just two communities, one can alternatively define si = ±1 to indicate the community to which node i belongs, which then leads to

where s is the column vector with elements si.
This function has the same form as the Hamiltonian
of an Ising spin glass
, a connection that has been exploited to create simple computer algorithms, for instance using simulated annealing
, to maximize the modularity. The general form of the modularity for arbitrary numbers of communities is equivalent to a Potts spin glass and similar algorithms can be developed for this case also.
one would find in the cluster if the network were a random network with the same number of nodes and where
each node keeps its degree, but edges are otherwise randomly attached. This random null model implicitly assumes that
each node can get attached to any other node of the network. Such assumption is however unreasonable if the network
is very large, as the horizon of a node includes a small part of the network, ignoring most of it.
Moreover, this implies that the expected number of edges between two groups of nodes decreases
if the size of the network increases. So, if a network is large enough, the expected number of edges between two groups
of nodes in modularity's null model may be smaller than one. If this happens, a single edge between the two clusters
would be interpreted by modularity as a sign of a strong correlation between the two clusters, and optimizing modularity
would lead to the merge of the two clusters, independently of the clusters' features. So, even weakly interconnected complete graphs, which
have the highest possible density of internal edges, and represent the best identifiable communities,
would be merged by modularity optimization if the network is sufficiently large.
For this reason, optimizing modularity in large networks would fail to resolve small communities, even when they are well defined. This bias
is inevitable for methods like modularity optimization, which rely on a global null model.
Complex network
In the context of network theory, a complex network is a graph with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in real graphs...
or graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. It measures the strength of division of a network into modules (also called groups, clusters or communities). Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. Modularity is often used in optimisation methods for detecting community structure
Community structure
In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally...
in networks.
Motivation
Many scientifically important problems can be represented and empirically studied using networks. For example, biological and social patterns, the world-wide web, metabolic networks, food webs, neural networks and pathological networks are a few examples of real world problems that can be mathematically represented and topologically studied to reveal some unexpected structural features . Most of these networks possess a certain community structure that has substantial importance in building an understanding regarding the dynamics of the network. For instance, a closely connected social community will imply a faster rate of transmission of information or rumor among them than a loosely connected community. Thus, if a network is represented by a number of individual nodes connected by links which signify a certain degree of interaction between the nodes, communities are defined as groups of densely interconnected nodes that are only sparsely connected with the rest of the network. Hence, it may be imperative to identify the communities in networks since the communities may have quite different properties such as node degree, clustering coefficient, betweenness, centrality . etc, from that of the average network. Modularity is one such measure, which when maximized; it leads to the appearance of communities in a given network.Definition
Modularity is the fraction of the edges that fall within the given groups minus the expected such fraction if edges were distributed at random. The value of the modularity lies in the range [−1,1]. It is positive if the number of edges within groups exceeds the number expected on the basis of chance. For a given division of the network's vertices into some modules, modularity reflects the concentration of nodes within modules compared with random distribution of links between all nodes regardless of modules.There are different methods for calculating modularity. In the most common version of the concept, the randomization of the edges is done so as to preserve the degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of each vertex. Let us consider a graph with
 nodes
nodesVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
and
 links (edges) such that the graph can be partitioned into 2 communities using a membership variable
links (edges) such that the graph can be partitioned into 2 communities using a membership variable  . If a node
. If a node  belongs to community 1,
belongs to community 1,  , or if
, or if 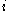 belongs to community 2,
belongs to community 2, 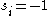 . Let the adjacency matrix
. Let the adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
for the network be represented by
 , where
, where 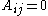 means there's no edge (no interaction) between nodes
means there's no edge (no interaction) between nodes 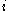 and
and 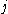 and
and 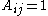 means there is an edge between the two. Also for simplicity we consider an undirected network. Thus
means there is an edge between the two. Also for simplicity we consider an undirected network. Thus 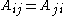 . (It is important to note that multiple edges may exist between 2 nodes and here we assess the simplest case).
. (It is important to note that multiple edges may exist between 2 nodes and here we assess the simplest case).Modularity Q is then defined as the fraction of edges that fall within group 1 or 2, minus the expected number of edges within group 1 and 2 for a random graph with same node degree distribution as the given network.
The expected number of edges shall be computed using the concept of Configuration Models . The configuration model is a randomized realization of a particular network. Given a network with n nodes, where each node i has a node degree ki, the configuration model cuts each edge into 2 halves, and then each half edge, called a stub, is rewired randomly with any other stub in the network even allowing self loops. Thus, even though the node degree distribution of the graph remains intact, the configuration model results in a completely random network.
Let the total number of stubs be ln
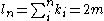
Now, if we randomly select two nodes i and j with node degrees ki and kj respectively and rewire the stubsfor these 2 nodes, then,
Expected [Full edges between i and j] = (Full edges between i and j)/(Total number of rewirings possible) (2)
Total number of rewritings possible = number of stubs remaining after choosing a particular stub
= ln-1= l n for large n
Thus, Expected [Number of full edges between i and j]=(ki* kj)/ln =(ki kj)/2m.
Hence, the actual number of edges between i and j minus expected number of edges between them is Aij-(ki kj )/2m. Thus using
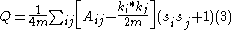
It is important to note that (3) holds good for partitioning into 2 communities only. Hierarchical partitioning (i.e. partitioning into 2 communities, then the 2 sub-communities further partitioned into 2 smaller sub communities only to maximize Q) is a possible approach to identify multiple communities in a network. Additionally, (3) can be generalized for partitioning a network into c communities. .
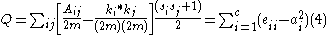
where eii is the fraction of edges with both end vertices in the same community i.
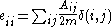
and ai is the fraction of edges with at least one end vertex in community i.

Example of multiple community detection
We consider an undirected network with 10 nodes and 12 edges and the following adjacency matrix.| Node ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
The communities in the graph are represented by the red, green and blue node clusters in Fig 1. The optimal community partitions are depicted in Fig 2.
Matrix formulation
An alternative formulation of the modularity, useful particularly in spectral optimization algorithms, is as follows. Define Sir to be 1 if vertex i belongs to group r and zero otherwise. Then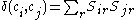
and hence
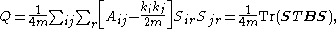
where S is the (non-square) matrix having elements Sir and B is the so-called modularity matrix, which has elements
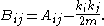
All rows and columns of the modularity matrix sum to zero, which means that the modularity of an undivided network is also always zero.
For networks divided into just two communities, one can alternatively define si = ±1 to indicate the community to which node i belongs, which then leads to

where s is the column vector with elements si.
This function has the same form as the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of an Ising spin glass
Spin glass
A spin glass is a magnet with frustrated interactions, augmented by stochastic disorder, where usually ferromagnetic and antiferromagnetic bonds are randomly distributed...
, a connection that has been exploited to create simple computer algorithms, for instance using simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
, to maximize the modularity. The general form of the modularity for arbitrary numbers of communities is equivalent to a Potts spin glass and similar algorithms can be developed for this case also.
Resolution limit
Modularity compares the number of edges inside a cluster with the expected number of edges thatone would find in the cluster if the network were a random network with the same number of nodes and where
each node keeps its degree, but edges are otherwise randomly attached. This random null model implicitly assumes that
each node can get attached to any other node of the network. Such assumption is however unreasonable if the network
is very large, as the horizon of a node includes a small part of the network, ignoring most of it.
Moreover, this implies that the expected number of edges between two groups of nodes decreases
if the size of the network increases. So, if a network is large enough, the expected number of edges between two groups
of nodes in modularity's null model may be smaller than one. If this happens, a single edge between the two clusters
would be interpreted by modularity as a sign of a strong correlation between the two clusters, and optimizing modularity
would lead to the merge of the two clusters, independently of the clusters' features. So, even weakly interconnected complete graphs, which
have the highest possible density of internal edges, and represent the best identifiable communities,
would be merged by modularity optimization if the network is sufficiently large.
For this reason, optimizing modularity in large networks would fail to resolve small communities, even when they are well defined. This bias
is inevitable for methods like modularity optimization, which rely on a global null model.

