
Milnor map
Encyclopedia
In mathematics, Milnor maps are named in honor of John Milnor
, who introduced them to topology
and algebraic geometry
in his book Singular Points of Complex Hypersurfaces (Princeton University Press, 1968) and earlier lectures. The most studied Milnor maps are actually fibration
s, and the phrase Milnor fibration is more commonly encountered in the mathematical literature. The general definition is as follows.
Let be a non-constant polynomial function of
be a non-constant polynomial function of  complex variables
complex variables
 such that
such that  , so that the set
, so that the set 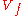 of all complex
of all complex  -vectors
-vectors  with
with  is a complex hypersurface of complex dimension
is a complex hypersurface of complex dimension
 containing the origin of complex
containing the origin of complex  -space. (For instance, if
-space. (For instance, if  then
then 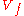 is a complex plane curve containing
is a complex plane curve containing 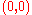 .) The argument
.) The argument
of is the function
is the function
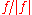 mapping the complement of
mapping the complement of 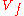 in complex
in complex  -space to the unit circle
-space to the unit circle
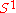 in C. For any real radius
in C. For any real radius  , the restriction of the argument of
, the restriction of the argument of  to the complement of
to the complement of 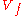 in the real
in the real  -sphere with center at the origin and radius
-sphere with center at the origin and radius  is the Milnor map of
is the Milnor map of  at radius
at radius  .
.
Milnor's Fibration Theorem states that, for every such that the origin is a singular point
such that the origin is a singular point
of the hypersurface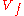 (in particular, for every non-constant square-free polynomial
(in particular, for every non-constant square-free polynomial
 of two variables, the case of plane curves), then for
of two variables, the case of plane curves), then for  sufficiently small,
sufficiently small,
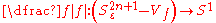
is a fibration. Each fiber is a non-compact differentiable manifold
of real dimension , and the closure of each fiber is a compact manifold
, and the closure of each fiber is a compact manifold
with boundary bounded by the intersection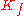 of
of 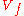 with the
with the  -sphere of sufficiently small radius. Furthermore, this compact manifold with boundary, which is known as the Milnor fiber (of the isolated singular point of
-sphere of sufficiently small radius. Furthermore, this compact manifold with boundary, which is known as the Milnor fiber (of the isolated singular point of 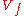 at the origin), is diffeomorphic to the intersection of the
at the origin), is diffeomorphic to the intersection of the  -ball (bounded by the small
-ball (bounded by the small  -sphere) with the (non-singular) hypersurface
-sphere) with the (non-singular) hypersurface 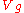 where
where 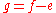 and
and  is any sufficiently small non-zero complex number. This small piece of hypersurface is also called a Milnor fiber.
is any sufficiently small non-zero complex number. This small piece of hypersurface is also called a Milnor fiber.
Milnor maps at other radii are not always fibrations, but they still have many interesting properties. For most (but not all) polynomials, the Milnor map at infinity (that is, at any sufficiently large radius) is again a fibration.
The Milnor map of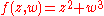 at any radius is a fibration; this construction gives the trefoil knot
at any radius is a fibration; this construction gives the trefoil knot
its structure as a fibered knot
.
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
, who introduced them to topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
in his book Singular Points of Complex Hypersurfaces (Princeton University Press, 1968) and earlier lectures. The most studied Milnor maps are actually fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s, and the phrase Milnor fibration is more commonly encountered in the mathematical literature. The general definition is as follows.
Let
 be a non-constant polynomial function of
be a non-constant polynomial function of  complex variables
complex variablesComplex variables
In mathematics, the term complex variables may be taken to mean one of* Complex analysis* Several complex variables* Quaternion variable* Motor variable* Multicomplex numbers* Hypercomplex numbers* Tricomplex numbers...
 such that
such that  , so that the set
, so that the set 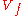 of all complex
of all complex  -vectors
-vectors  with
with  is a complex hypersurface of complex dimension
is a complex hypersurface of complex dimensionComplex dimension
In mathematics, complex dimension usually refers to the dimension of a complex manifold M, or complex algebraic variety V. If the complex dimension is d, the real dimension will be 2d...
 containing the origin of complex
containing the origin of complex  -space. (For instance, if
-space. (For instance, if  then
then 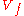 is a complex plane curve containing
is a complex plane curve containing 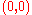 .) The argument
.) The argumentArgument
In philosophy and logic, an argument is an attempt to persuade someone of something, or give evidence or reasons for accepting a particular conclusion.Argument may also refer to:-Mathematics and computer science:...
of
 is the function
is the function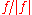 mapping the complement of
mapping the complement of 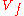 in complex
in complex  -space to the unit circle
-space to the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
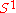 in C. For any real radius
in C. For any real radius  , the restriction of the argument of
, the restriction of the argument of  to the complement of
to the complement of 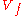 in the real
in the real  -sphere with center at the origin and radius
-sphere with center at the origin and radius  is the Milnor map of
is the Milnor map of  at radius
at radius  .
.Milnor's Fibration Theorem states that, for every
 such that the origin is a singular point
such that the origin is a singular pointSingular point of a curve
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...
of the hypersurface
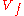 (in particular, for every non-constant square-free polynomial
(in particular, for every non-constant square-free polynomialSquare-free polynomial
In mathematics, a square-free polynomial is a polynomial with no square factors, i.e, f \in F[x] is square-free if and only if b^2 \nmid f for every b \in F[x] with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2...
 of two variables, the case of plane curves), then for
of two variables, the case of plane curves), then for  sufficiently small,
sufficiently small,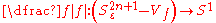
is a fibration. Each fiber is a non-compact differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
of real dimension
 , and the closure of each fiber is a compact manifold
, and the closure of each fiber is a compact manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with boundary bounded by the intersection
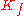 of
of 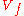 with the
with the  -sphere of sufficiently small radius. Furthermore, this compact manifold with boundary, which is known as the Milnor fiber (of the isolated singular point of
-sphere of sufficiently small radius. Furthermore, this compact manifold with boundary, which is known as the Milnor fiber (of the isolated singular point of 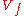 at the origin), is diffeomorphic to the intersection of the
at the origin), is diffeomorphic to the intersection of the  -ball (bounded by the small
-ball (bounded by the small  -sphere) with the (non-singular) hypersurface
-sphere) with the (non-singular) hypersurface 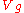 where
where 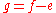 and
and  is any sufficiently small non-zero complex number. This small piece of hypersurface is also called a Milnor fiber.
is any sufficiently small non-zero complex number. This small piece of hypersurface is also called a Milnor fiber.Milnor maps at other radii are not always fibrations, but they still have many interesting properties. For most (but not all) polynomials, the Milnor map at infinity (that is, at any sufficiently large radius) is again a fibration.
The Milnor map of
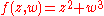 at any radius is a fibration; this construction gives the trefoil knot
at any radius is a fibration; this construction gives the trefoil knotTrefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
its structure as a fibered knot
Fibered knot
A knot or link Kin the 3-dimensional sphere S^3 is called fibered or fibred if there is a 1-parameter family F_t of Seifert surfaces for K, where the parameter t runs through the points of the unit circle S^1, such that if s is not equal to t...
.

