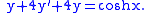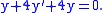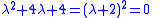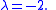Method of variation of parameters
Encyclopedia
In mathematics
, variation of parameters, also known as variation of constants, is a general method to solve inhomogeneous linear
ordinary differential equation
s. It was developed by Joseph Louis Lagrange
.
For first-order inhomogeneous linear differential equations it is usually possible to find solutions via integrating factor
s or undetermined coefficients
with considerably less effort, although those methods leverage heuristics that involve guessing and don't work for all inhomogenous linear differential equations.
Variation of parameters extends to linear partial differential equations as well, specifically to inhomogeneous problems for linear evolution equations like the heat equation
, wave equation
, and vibrating plate
equation. In this setting, the method is more often known as Duhamel's principle
, named after Jean-Marie Duhamel
who first applied the method to solve the inhomogeneous heat equation. Sometimes variation of parameters itself is called Duhamel's principle and vice-versa.
 (i)
(i)
let be a fundamental system of the corresponding homogeneous equation
be a fundamental system of the corresponding homogeneous equation
 (ii)
(ii)
Then a particular solution
to the non-homogeneous equation is given by
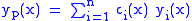 (iii)
(iii)
where the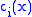 are continuous functions which satisfy the equations
are continuous functions which satisfy the equations
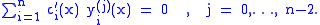 (iv)
(iv)
By substituting (iii) into (i) and applying (iv) it follows that (v)
(v)
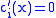 for all x and i is the only way to satisfy the condition, since all
for all x and i is the only way to satisfy the condition, since all 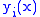 are linearly independent. It implies that all
are linearly independent. It implies that all  are independent of x in the homogeneous case b(x)=0. )
are independent of x in the homogeneous case b(x)=0. )
This linear system of n equations can then be solved using Cramer's rule
yielding
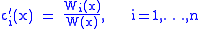
where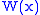 is the Wronskian determinant of the fundamental system and
is the Wronskian determinant of the fundamental system and 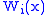 is the Wronskian determinant of the fundamental system with the i-th column replaced by
is the Wronskian determinant of the fundamental system with the i-th column replaced by 
The particular solution to the non-homogeneous equation can then be written as

We want to find the general solution to the differential equation, that is, we want to find solutions to the homogeneous differential equation
From the characteristic equation
Since we have a repeated root, we have to introduce a factor of x for one solution to ensure linear independence.
So, we obtain u1 = e−2x, and u2 = xe−2x. The Wronskian
of these two functions is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, variation of parameters, also known as variation of constants, is a general method to solve inhomogeneous linear
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. It was developed by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
.
For first-order inhomogeneous linear differential equations it is usually possible to find solutions via integrating factor
Integrating factor
In mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus, in this case often multiplying through by an...
s or undetermined coefficients
Method of undetermined coefficients
In mathematics, the method of undetermined coefficients, also known as the lucky guess method, is an approach to finding a particular solution to certain inhomogeneous ordinary differential equations and recurrence relations...
with considerably less effort, although those methods leverage heuristics that involve guessing and don't work for all inhomogenous linear differential equations.
Variation of parameters extends to linear partial differential equations as well, specifically to inhomogeneous problems for linear evolution equations like the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, and vibrating plate
Vibrating plate
In solid mechanics, a branch of mathematics and physics, a plate is modeled as a two-dimensional elastic body whose potential energy depends on how it is bent from a planar configuration, rather than how it is stretched . A vibrating plate can be modeled in a manner analogous to a vibrating drum...
equation. In this setting, the method is more often known as Duhamel's principle
Duhamel's principle
In mathematics, and more specifically in partial differential equations, Duhamel's principle is a general method for obtaining solutions to inhomogeneous linear evolution equations like the heat equation, wave equation, and vibrating plate equation...
, named after Jean-Marie Duhamel
Jean-Marie Duhamel
Jean-Marie Constant Duhamel was a noted French mathematician and physicist. His studies were affected by troubles of the Napoleonic era. He went on to form his own school École Sainte-Barbe. Duhamel's principle is named for him. He was primarily a mathematician but did studies on the mathematics...
who first applied the method to solve the inhomogeneous heat equation. Sometimes variation of parameters itself is called Duhamel's principle and vice-versa.
Description of method
Given an ordinary non-homogeneous linear differential equation of order n (i)
(i)let
 be a fundamental system of the corresponding homogeneous equation
be a fundamental system of the corresponding homogeneous equation (ii)
(ii)Then a particular solution
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
to the non-homogeneous equation is given by
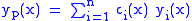 (iii)
(iii)where the
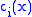 are continuous functions which satisfy the equations
are continuous functions which satisfy the equations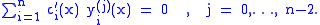 (iv)
(iv)By substituting (iii) into (i) and applying (iv) it follows that
 (v)
(v) 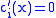 for all x and i is the only way to satisfy the condition, since all
for all x and i is the only way to satisfy the condition, since all 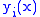 are linearly independent. It implies that all
are linearly independent. It implies that all  are independent of x in the homogeneous case b(x)=0. )
are independent of x in the homogeneous case b(x)=0. )This linear system of n equations can then be solved using Cramer's rule
Cramer's rule
In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
yielding
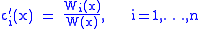
where
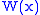 is the Wronskian determinant of the fundamental system and
is the Wronskian determinant of the fundamental system and 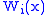 is the Wronskian determinant of the fundamental system with the i-th column replaced by
is the Wronskian determinant of the fundamental system with the i-th column replaced by 
The particular solution to the non-homogeneous equation can then be written as

Specific second order equation
Let us solveWe want to find the general solution to the differential equation, that is, we want to find solutions to the homogeneous differential equation
From the characteristic equation
Since we have a repeated root, we have to introduce a factor of x for one solution to ensure linear independence.
So, we obtain u1 = e−2x, and u2 = xe−2x. The Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
of these two functions is
-

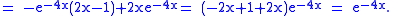
Because the Wronskian is non-zero, the two functions are linearly independent, so this is in fact the general solution for the homogeneous differential equation (and not a mere subset of it).
We seek functions A(x) and B(x) so A(x)u1 + B(x)u2 is a general solution of the non-homogeneous equation. We need only calculate the integrals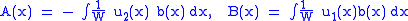
that is,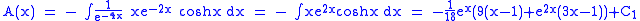
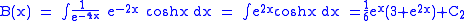
where and
and  are constants of integration.
are constants of integration.
General second order equation
We have a differential equation of the form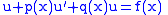
and we define the linear operator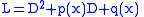
where D represents the differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. We therefore have to solve the equation for
for 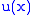 , where
, where  and
and 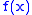 are known.
are known.
We must solve first the corresponding homogeneous equation: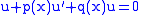
by the technique of our choice. Once we've obtained two linearly independent solutions to this homogeneous differential equation (because this ODE is second-order) — call them u1 and u2 — we can proceed with variation of parameters.
Now, we seek the general solution to the differential equation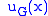 which we assume to be of the form
which we assume to be of the form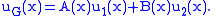
Here,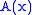 and
and 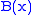 are unknown and
are unknown and 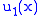 and
and 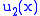 are the solutions to the homogeneous equation. Observe that if
are the solutions to the homogeneous equation. Observe that if 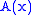 and
and  are constants, then
are constants, then  . We desire A=A(x) and B=B(x) to be of the form
. We desire A=A(x) and B=B(x) to be of the form
Now,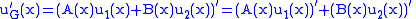
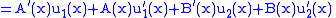
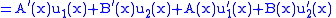
and since we have required the above condition, then we have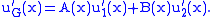
Differentiating again (omitting intermediary steps)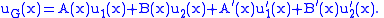
Now we can write the action of L upon uG as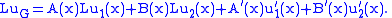
Since u1 and u2 are solutions, then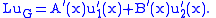
We have the system of equations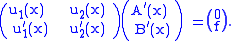
Expanding,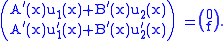
So the above system determines precisely the conditions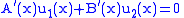

We seek A(x) and B(x) from these conditions, so, given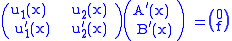
we can solve for (A′(x), B′(x))T, so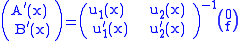

where W denotes the WronskianWronskianIn mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
of u1 and u2. (We know that W is nonzero, from the assumption that u1 and u2 are linearly independent.)
So,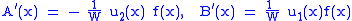
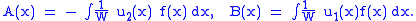
While homogeneous equations are relatively easy to solve, this method allows the calculation of the coefficients of the general solution of the inhomogeneous equation, and thus the complete general solution of the inhomogeneous equation can be determined.
Note that and
and 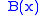 are each determined only up to an arbitrary additive constant (the constant of integration); one would expect two constants of integration because the original equation was second order. Adding a constant to
are each determined only up to an arbitrary additive constant (the constant of integration); one would expect two constants of integration because the original equation was second order. Adding a constant to 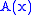 or
or 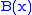 does not change the value of
does not change the value of 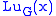 because
because  is linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
is linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
.
External links
- Online Notes / Proof by Paul Dawkins, Lamar UniversityLamar UniversityLamar University, often referred to as Lamar or LU, is a comprehensive coeducational public research university located in Beaumont, Texas, United States. Lamar confers bachelors, masters and doctoral degrees and is classified as a Doctoral Research University by the Carnegie Commission on Higher...
. - PlanetMath page.
- Motivation of method via celestial mechanics
- Online Notes / Proof by Paul Dawkins, Lamar University