Mean annual increment
Encyclopedia
The mean annual increment (MAI) or mean annual growth refers to the average growth per year a tree or stand of trees has exhibited/experienced to a specified age. For example, a 20-year old tree that has a diameter at breast height
(dbh) of 10.0 inches has an MAI of 0.5 inches/year. MAI is calculated as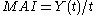 where Y(t) = yield at time t. Because the typical growth patterns of most trees is sigmoidal
where Y(t) = yield at time t. Because the typical growth patterns of most trees is sigmoidal
, the MAI starts out small, increases to a maximum value as the tree matures, then declines slowly over the remainder of the tree's life. Throughout this, the MAI always remains positive. MAI differs from periodic annual increment
(PAI) because the PAI is simply the growth for one specific year or any other specified length of time.
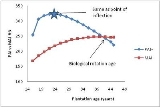
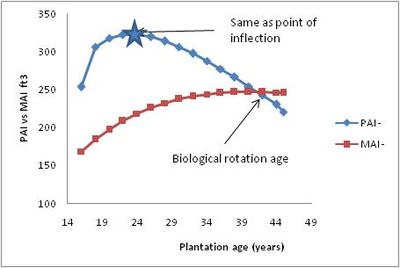 The point where the MAI and PAI meet is typically referred to as the biological rotation age. This is the age at which the tree or stand would be harvested if the management objective is to maximize long-term yield. The proof of this definition is shown by differentiating MAI(t) with respect to t, and is shown by Husch, Miller, and Beers
The point where the MAI and PAI meet is typically referred to as the biological rotation age. This is the age at which the tree or stand would be harvested if the management objective is to maximize long-term yield. The proof of this definition is shown by differentiating MAI(t) with respect to t, and is shown by Husch, Miller, and Beers
Diameter at breast height
Diameter at breast height, or DBH, is a standard method of expressing the diameter of the trunk or bole of a standing tree. DBH is one of the most common dendrometric measurements....
(dbh) of 10.0 inches has an MAI of 0.5 inches/year. MAI is calculated as
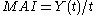 where Y(t) = yield at time t. Because the typical growth patterns of most trees is sigmoidal
where Y(t) = yield at time t. Because the typical growth patterns of most trees is sigmoidalSigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
, the MAI starts out small, increases to a maximum value as the tree matures, then declines slowly over the remainder of the tree's life. Throughout this, the MAI always remains positive. MAI differs from periodic annual increment
Periodic annual increment
Periodic annual increment , is a forestry term that describes the change in the size of a tree between the beginning and ending of a growth period, divided by the number of years that was designated as the growing period . For sigmoid growth, the graph of PAI increases rapidly and then quickly...
(PAI) because the PAI is simply the growth for one specific year or any other specified length of time.


