Markov number
Encyclopedia
A Markov number or Markoff number is a positive integer x, y or z that is part of a solution to the Markov Diophantine equation
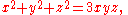
studied by .
The first few Markov numbers are
appearing as coordinates of the Markov triples
, (1, 1, 2), (1, 2, 5), (1, 5, 13), (2, 5, 29), (1, 13, 34), (1, 34, 89), (2, 29, 169), (5, 13, 194), (1, 89, 233), (5, 29, 433), (89, 233, 610), etc.
There are infinitely many Markov numbers and Markov triples.
All the Markov numbers on the regions adjacent to 2's region are odd-indexed Pell number
s (or numbers n such that 2n2 − 1 is a square), and all the Markov numbers on the regions adjacent to 1's region are odd-indexed Fibonacci number
s . Thus, there are infinitely many Markov triples of the form

where Fx is the xth Fibonacci number. Likewise, there are infinitely many Markov triples of the form
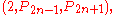
where Px is the xth Pell number
.
 consists of three distinct integers.
consists of three distinct integers.
The unicity conjecture states that for a given Markov number , there is exactly one normalized solution having
, there is exactly one normalized solution having  as its largest element.
as its largest element.
Odd Markov numbers are 1 more than multiples of 4, while even Markov numbers are 2 more than multiples of 32.
In his 1982 paper, Don Zagier
conjectured that the nth Markov number is asymptotically given by
Moreover he pointed out that , an extremely good approximation of the original Diophantine equation, is equivalent to
, an extremely good approximation of the original Diophantine equation, is equivalent to 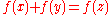 with f(t) = arcosh(3t/2).
with f(t) = arcosh(3t/2).
The nth Lagrange number
can be calculated from the nth Markov number with the formula
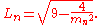
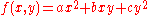
is an indefinite binary quadratic form with real coefficients, then there are integers x, y for which it takes a nonzero value of absolute value at most
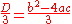
unless f is a constant times a form
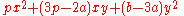
where (p, q, r) is a Markov triple and
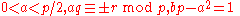
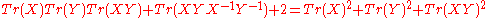
so that if Tr(XYX−1Y−1)=−2 then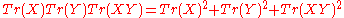
In particular if X and Y also have integer entries then Tr(X)/3, Tr(Y)/3, and Tr(XY)/3 are a Markov triple. If XYZ = 1 then Tr(XY) = Tr(Z), so more symmetrically if X, Y, and Z are in SL2(Z) with XYZ = 1 and the commutator of two of them has trace −2, then their traces/3 are a Markov triple.
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
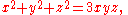
studied by .
The first few Markov numbers are
- 1, 2, 5, 1313 (number)13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 3434 (number)34 is the natural number following 33 and preceding 35.-In mathematics:34 is the ninth distinct semiprime and has four divisors including unity and itself. Its neighbors, 33 and 35, also are distinct semiprimes, having four divisors each, and 34 is the smallest number to be surrounded by numbers...
, 89, 169169 (number)169 is the natural number following 168 and preceding 170.-In mathematics:* 169 is an odd number* 169 is a square number. 13 x 13 = 169, and the reverse 31 x 31 = 961...
, 194194 (number)194 is the natural number following 193 and preceding 195.-In mathematics:* 194 is an even number* 194 is a composite number* 194 is a deficient number, as 100 is less than 194...
, 233233 (number)233 is the natural number between 232 and 234. It is also a prime number.-In mathematics:233 is an irregular prime, a full reptend prime, a cousin prime, a Chen prime, a Fibonacci prime and a sexy prime. It is the 13th Fibonacci number. It is an Eisenstein prime of the form 3n - 1 with no...
, 433, 610, 985, 1325, ...
appearing as coordinates of the Markov triples
, (1, 1, 2), (1, 2, 5), (1, 5, 13), (2, 5, 29), (1, 13, 34), (1, 34, 89), (2, 29, 169), (5, 13, 194), (1, 89, 233), (5, 29, 433), (89, 233, 610), etc.
There are infinitely many Markov numbers and Markov triples.
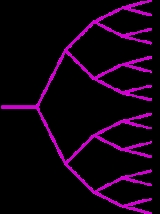
Markov tree
There are two simple ways to obtain a new Markov triple from an old one (x, y, z). First, one may permute the 3 numbers x,y,z, so in particular one can normalize the triples so that x ≤ y ≤ z. Second, if (x, y, z) is a Markov triple then so is (x, y, 3xy − z). Applying this operation twice returns the same triple one started with. Joining each normalized Markov triple to the 1, 2, or 3 normalized triples one can obtain from this gives a graph starting from (1,1,1) as in the diagram. This graph is connected; in other words every Markov triple can be connected to (1,1,1) by a sequence of these operations. If we start, as an example, with (1, 5, 13) we get its three neighbors (5, 13, 194), (1, 13, 34) and (1, 2, 5) in the Markov tree if x is set to 1, 5 and 13, respectively. For instance, starting with (1, 1, 2) and trading y and z before each iteration of the transform lists Markov triples with Fibonacci numbers. Starting with that same triplet and trading x and z before each iteration gives the triples with Pell numbers.All the Markov numbers on the regions adjacent to 2's region are odd-indexed Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s (or numbers n such that 2n2 − 1 is a square), and all the Markov numbers on the regions adjacent to 1's region are odd-indexed Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s . Thus, there are infinitely many Markov triples of the form

where Fx is the xth Fibonacci number. Likewise, there are infinitely many Markov triples of the form
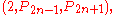
where Px is the xth Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
.
Other properties
Aside from the two smallest triples, every Markov triple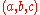 consists of three distinct integers.
consists of three distinct integers.The unicity conjecture states that for a given Markov number
 , there is exactly one normalized solution having
, there is exactly one normalized solution having  as its largest element.
as its largest element.Odd Markov numbers are 1 more than multiples of 4, while even Markov numbers are 2 more than multiples of 32.
In his 1982 paper, Don Zagier
Don Zagier
Don Bernard Zagier is an American mathematician whose main area of work is number theory. He is currently one of the directors of the Max Planck Institute for Mathematics in Bonn, Germany, and a professor at the Collège de France in Paris, France.He was born in Heidelberg, Germany...
conjectured that the nth Markov number is asymptotically given by

Moreover he pointed out that
 , an extremely good approximation of the original Diophantine equation, is equivalent to
, an extremely good approximation of the original Diophantine equation, is equivalent to 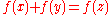 with f(t) = arcosh(3t/2).
with f(t) = arcosh(3t/2).The nth Lagrange number
Lagrange number
In mathematics, the Lagrange numbers are a sequence of numbers that appear in bounds relating to the approximation of irrational numbers by rational numbers...
can be calculated from the nth Markov number with the formula
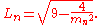
Markov's theorem
showed that if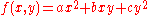
is an indefinite binary quadratic form with real coefficients, then there are integers x, y for which it takes a nonzero value of absolute value at most
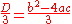
unless f is a constant times a form
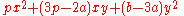
where (p, q, r) is a Markov triple and
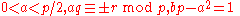
Matrices
If X and Y are in SL2(C) then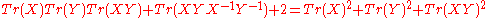
so that if Tr(XYX−1Y−1)=−2 then
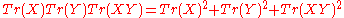
In particular if X and Y also have integer entries then Tr(X)/3, Tr(Y)/3, and Tr(XY)/3 are a Markov triple. If XYZ = 1 then Tr(XY) = Tr(Z), so more symmetrically if X, Y, and Z are in SL2(Z) with XYZ = 1 and the commutator of two of them has trace −2, then their traces/3 are a Markov triple.

