
Lagrange number
Encyclopedia
In mathematics
, the Lagrange numbers are a sequence of numbers that appear in bounds relating to the approximation of irrational numbers by rational numbers. They are linked to Hurwitz's theorem
.

This was an improvement on Dirichlet's result which had 1/q2 on the right hand side. The above result is best possible since the golden ratio
φ is irrational but if we replace √5 by any larger number in the above expression then we will only be able to find finitely many rational numbers that satisfy the inequality for α = φ.
However, Hurwitz also showed that if we omit the number φ, and numbers derived from it, then we can increase the number √5, in fact he showed we may replace it with 2√2. Again this new bound is best possible in the new setting, but this time the number √2 is the problem. If we don't allow √2 then we can increase the number on the right hand side of the inequality from 2√2 to (√221)/5. Repeating this process we get an infinite sequence of numbers √5, 2√2, (√221)/5, ... which converge to 3, called the Lagrange numbers, named after Joseph Louis Lagrange
.
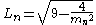
where mn is the nth Markov number
, that is the nth smallest integer m such that the equation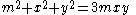
has a solution in positive integers x and y.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lagrange numbers are a sequence of numbers that appear in bounds relating to the approximation of irrational numbers by rational numbers. They are linked to Hurwitz's theorem
Hurwitz's theorem (number theory)
In number theory, Hurwitz's theorem, named after Adolf Hurwitz, gives a bound on a Diophantine approximation. The theorem states that for every irrational number ξ there are infinitely many rationals m/n such that...
.
Definition
Hurwitz improved Dirichlet's criterion on irrationality to the statement that a real number α is irrational if and only if there are infinitely many rational numbers p/q, written in lowest terms, such that
This was an improvement on Dirichlet's result which had 1/q2 on the right hand side. The above result is best possible since the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ is irrational but if we replace √5 by any larger number in the above expression then we will only be able to find finitely many rational numbers that satisfy the inequality for α = φ.
However, Hurwitz also showed that if we omit the number φ, and numbers derived from it, then we can increase the number √5, in fact he showed we may replace it with 2√2. Again this new bound is best possible in the new setting, but this time the number √2 is the problem. If we don't allow √2 then we can increase the number on the right hand side of the inequality from 2√2 to (√221)/5. Repeating this process we get an infinite sequence of numbers √5, 2√2, (√221)/5, ... which converge to 3, called the Lagrange numbers, named after Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
.
Relation to Markov numbers
The nth Lagrange number Ln is given by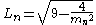
where mn is the nth Markov number
Markov number
A Markov number or Markoff number is a positive integer x, y or z that is part of a solution to the Markov Diophantine equationx^2 + y^2 + z^2 = 3xyz,\,studied by .The first few Markov numbers are...
, that is the nth smallest integer m such that the equation
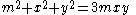
has a solution in positive integers x and y.
External links
- Lagrange number. From MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
at Wolfram Research. - Introduction to Diophantine methods irrationality and trancendence - Online lecture notes by Michel Waldschmidt, Lagrange Numbers on pp.24-26.

