
Mark Mahowald
Encyclopedia
Mark E. Mahowald is an American
mathematician
known for work in algebraic topology
.
in 1955 under the direction of Bernard Russel Gelbaum with a thesis on Measure in Groups. In the sixties, he became professor at Syracuse University
and around 1963 he went to Northwestern University
in Chicago, where he is now a professor emeritus.
, especially using the Adams spectral sequence
at the prime 2. He is known for constructing one of the first known infinite families of elements in the stable homotopy groups of spheres by showing that the classes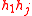 survive the Adams spectral sequence for
survive the Adams spectral sequence for  . In addition, he made extensive computations of the structure of the Adams spectral sequence and the 2-primary stable homotopy groups of spheres up to dimension 64 together with Barratt, Tangora and Kochman. Using these computations, he could show that a manifold of Kervaire invariant 1 exists in dimension 62.
. In addition, he made extensive computations of the structure of the Adams spectral sequence and the 2-primary stable homotopy groups of spheres up to dimension 64 together with Barratt, Tangora and Kochman. Using these computations, he could show that a manifold of Kervaire invariant 1 exists in dimension 62.
In addition, he contributed to the chromatic picture of the homotopy groups of spheres: His earlier work contains much on the image of the J-homomorphism
and recent work together with Goerss, Henn, Karamanov and Rezk does computations in stable homotopy localized at the Morava K-theory
K(2).
Besides the work on the homotopy groups of spheres and related spaces, he did important work on Thom spectra. This work was used heavily in the proof of the nilpotence theorem
by Devinatz, Hopkins
and Smith.
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
known for work in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
Life
He received his Ph.D. from University of MinnesotaUniversity of Minnesota
The University of Minnesota, Twin Cities is a public research university located in Minneapolis and St. Paul, Minnesota, United States. It is the oldest and largest part of the University of Minnesota system and has the fourth-largest main campus student body in the United States, with 52,557...
in 1955 under the direction of Bernard Russel Gelbaum with a thesis on Measure in Groups. In the sixties, he became professor at Syracuse University
Syracuse University
Syracuse University is a private research university located in Syracuse, New York, United States. Its roots can be traced back to Genesee Wesleyan Seminary, founded by the Methodist Episcopal Church in 1832, which also later founded Genesee College...
and around 1963 he went to Northwestern University
Northwestern University
Northwestern University is a private research university in Evanston and Chicago, Illinois, USA. Northwestern has eleven undergraduate, graduate, and professional schools offering 124 undergraduate degrees and 145 graduate and professional degrees....
in Chicago, where he is now a professor emeritus.
Work
Much of Mahowald's most important works concerns the homotopy groups of spheresHomotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
, especially using the Adams spectral sequence
Adams spectral sequence
In mathematics, the Adams spectral sequence is a spectral sequence introduced by . Like all spectral sequences, it is a computational tool; it relates homology theory to what is now called stable homotopy theory...
at the prime 2. He is known for constructing one of the first known infinite families of elements in the stable homotopy groups of spheres by showing that the classes
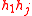 survive the Adams spectral sequence for
survive the Adams spectral sequence for  . In addition, he made extensive computations of the structure of the Adams spectral sequence and the 2-primary stable homotopy groups of spheres up to dimension 64 together with Barratt, Tangora and Kochman. Using these computations, he could show that a manifold of Kervaire invariant 1 exists in dimension 62.
. In addition, he made extensive computations of the structure of the Adams spectral sequence and the 2-primary stable homotopy groups of spheres up to dimension 64 together with Barratt, Tangora and Kochman. Using these computations, he could show that a manifold of Kervaire invariant 1 exists in dimension 62.In addition, he contributed to the chromatic picture of the homotopy groups of spheres: His earlier work contains much on the image of the J-homomorphism
J-homomorphism
In mathematics, the J-homomorphism is a mapping from the homotopy groups of the special orthogonal groups to the homotopy groups of spheres. It was defined by , extending a construction of .-Definition:...
and recent work together with Goerss, Henn, Karamanov and Rezk does computations in stable homotopy localized at the Morava K-theory
Morava K-theory
In stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s...
K(2).
Besides the work on the homotopy groups of spheres and related spaces, he did important work on Thom spectra. This work was used heavily in the proof of the nilpotence theorem
Nilpotence theorem
In algebraic topology, the nilpotence theorem gives a condition for an element of the coefficient ring of a ring spectrum to be nilpotent, in terms of complex cobordism. It was conjectured by and proved by .-Nishida's theorem:...
by Devinatz, Hopkins
Michael J. Hopkins
Michael Jerome Hopkins is an American mathematician known for work in algebraic topology.-Life:He received his Ph.D. from Northwestern University in 1984 under the direction of Mark Mahowald. In 1984 he also received his D.Phil...
and Smith.

