Margrabe's formula
Encyclopedia
In mathematical finance
, Margrabe's formula is an option
pricing formula. It applies to an option to exchange one risky asset for another risky asset at maturity.
Suppose S1(t) and S2(t) are the prices of two risky assets at time t, and that each has a constant continuous dividend yield qi. The option, C, that we wish to price gives the buyer the right, but not the obligation, to exchange the second asset for the first at the time of maturity T. In other words, its payoff, C(T), is max(0, S1(T) - S2(T)).
Margrabe's model of the market assumes only the existence of the two risky assets, whose prices, as usual, are assumed to follow a geometric Brownian motion
. The volatilities of these Brownian motions do not need to be constant, but it is important that the volatility of S1/S2, σ, is constant. In particular, the model does not assume the existence of a riskless asset (such as a zero-coupon bond) or any kind of interest rate
.
If the volatilities of Si 's are σi, then
, where ρ is the correlation coefficient of the Brownian motions of the Si 's.
Margrabe's formula states that the right price for the option at time 0 is:
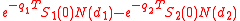
where N denotes the cumulative distribution function for a standard normal, d1 = (ln (S_1(0)/S_2(0)) + (q2 - q1 + σ2/2)T)/σ
, and d2 = d1 - σ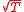
.
The formula is quickly proven by reducing the situation to one where we can apply the Black-Scholes formula. First, consider both assets as priced in units of S2 (this is called 'using S2 as numeraire
'); this means that a unit of the first asset now has is worth S1/S2 units of the second asset, and a unit of the second asset is worth 1. Under this change of numeraire pricing, the second asset is now a riskless asset and its dividend rate q2 is the interest rate. The payoff of the option, repriced under this change of numeraire, is max(0, S1(T)/S2(T) - 1). So the original option has become a call option
on the first asset (with its numeraire pricing) with a strike of 1 unit of the riskless asset. Note the dividend rate q1 of the first asset remains the same even with change of pricing.
Applying the Black-Scholes formula with these values as the appropriate inputs, e.g. initial asset value S1(0)/S2(0), interest rate q2, volatility σ, etc., gives us the price of the option under numeraire pricing. Since the resulting option price is in units of S2, multiplying through by S2(0) will undo our change of numeraire, and give us the price in our original currency, which is the formula above.
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, Margrabe's formula is an option
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
pricing formula. It applies to an option to exchange one risky asset for another risky asset at maturity.
Suppose S1(t) and S2(t) are the prices of two risky assets at time t, and that each has a constant continuous dividend yield qi. The option, C, that we wish to price gives the buyer the right, but not the obligation, to exchange the second asset for the first at the time of maturity T. In other words, its payoff, C(T), is max(0, S1(T) - S2(T)).
Margrabe's model of the market assumes only the existence of the two risky assets, whose prices, as usual, are assumed to follow a geometric Brownian motion
Geometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
. The volatilities of these Brownian motions do not need to be constant, but it is important that the volatility of S1/S2, σ, is constant. In particular, the model does not assume the existence of a riskless asset (such as a zero-coupon bond) or any kind of interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
.
If the volatilities of Si 's are σi, then
, where ρ is the correlation coefficient of the Brownian motions of the Si 's.Margrabe's formula states that the right price for the option at time 0 is:
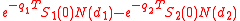
where N denotes the cumulative distribution function for a standard normal, d1 = (ln (S_1(0)/S_2(0)) + (q2 - q1 + σ2/2)T)/σ
, and d2 = d1 - σ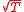.The formula is quickly proven by reducing the situation to one where we can apply the Black-Scholes formula. First, consider both assets as priced in units of S2 (this is called 'using S2 as numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
'); this means that a unit of the first asset now has is worth S1/S2 units of the second asset, and a unit of the second asset is worth 1. Under this change of numeraire pricing, the second asset is now a riskless asset and its dividend rate q2 is the interest rate. The payoff of the option, repriced under this change of numeraire, is max(0, S1(T)/S2(T) - 1). So the original option has become a call option
Call option
A call option, often simply labeled a "call", is a financial contract between two parties, the buyer and the seller of this type of option. The buyer of the call option has the right, but not the obligation to buy an agreed quantity of a particular commodity or financial instrument from the seller...
on the first asset (with its numeraire pricing) with a strike of 1 unit of the riskless asset. Note the dividend rate q1 of the first asset remains the same even with change of pricing.
Applying the Black-Scholes formula with these values as the appropriate inputs, e.g. initial asset value S1(0)/S2(0), interest rate q2, volatility σ, etc., gives us the price of the option under numeraire pricing. Since the resulting option price is in units of S2, multiplying through by S2(0) will undo our change of numeraire, and give us the price in our original currency, which is the formula above.