Mahler measure
Encyclopedia
In mathematics
, the Mahler measure M(p) of a polynomial
p is
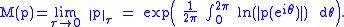
Here p is assumed complex
-valued and
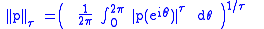
is the Lτ norm of p (although this is not a true norm for values of τ < 1).
It can be shown that if
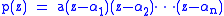
then
The Mahler measure of an algebraic number
α is defined as the Mahler measure of the minimal polynomial
of α over Q.
The measure is named after Kurt Mahler
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Mahler measure M(p) of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
p is
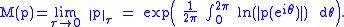
Here p is assumed complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued and
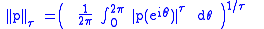
is the Lτ norm of p (although this is not a true norm for values of τ < 1).
It can be shown that if
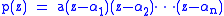
then
The Mahler measure of an algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
α is defined as the Mahler measure of the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of α over Q.
The measure is named after Kurt Mahler
Kurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
.
Properties
- The Mahler measure is multiplicative, i.e. M(pq) = M(p)M(q).
- (Kronecker's Theorem) If p is an irreducible monic integer polynomial with
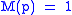, then either p(z)=z, or p is a cyclotomic polynomialCyclotomic polynomialIn algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
.