
Logrank test
Encyclopedia
In statistics
, the logrank test is a hypothesis test to compare the survival
distributions of two samples. It is a nonparametric test and appropriate to use when the data are right skewed and censored
(technically, the censoring must be non-informative). It is widely used in clinical trials to establish the efficacy of a new treatment compared to a control treatment when the measurement is the time to event (such as the time from initial treatment to a heart attack). The test is sometimes called the Mantel–Cox test, named after Nathan Mantel
and David Cox. The logrank test can also be viewed as a time stratified Cochran–Mantel–Haenszel test
.
The test was first proposed by Nathan Mantel
and was named the logrank test by Richard
and Julian Peto
.
Let j = 1, ..., J be the distinct times of observed events in either group. For each time , let
, let 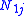 and
and  be the number of subjects "at risk" (have not yet had an event or been censored) at the start of period
be the number of subjects "at risk" (have not yet had an event or been censored) at the start of period 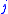 in the groups respectively. Let
in the groups respectively. Let  . Let
. Let 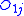 and
and  be the observed number of events in the groups respectively at time
be the observed number of events in the groups respectively at time 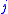 , and define
, and define 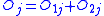 .
.
Given that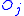 events happened across both groups at time
events happened across both groups at time 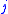 , under the null hypothesis (of the two groups having identical survival and hazard functions)
, under the null hypothesis (of the two groups having identical survival and hazard functions)  has the hypergeometric distribution with parameters
has the hypergeometric distribution with parameters 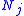 ,
,  , and
, and 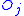 . This distribution has expected value
. This distribution has expected value 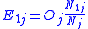 and variance
and variance 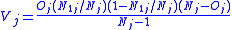 .
.
The logrank statistic compares each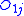 to its expectation
to its expectation  under the null hypothesis and is defined as
under the null hypothesis and is defined as

 test will reject the null hypothesis if
test will reject the null hypothesis if  where
where  is the upper
is the upper  quantile of the standard normal distribution. If the hazard ratio is
quantile of the standard normal distribution. If the hazard ratio is  , there are
, there are  total subjects,
total subjects,  is the probability a subject in either group will eventually have an event (so that
is the probability a subject in either group will eventually have an event (so that 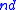 is the expected number of events at the time of the analysis), and the proportion of subjects randomized to each group is 50%, then the logrank statistic is approximately normal with mean
is the expected number of events at the time of the analysis), and the proportion of subjects randomized to each group is 50%, then the logrank statistic is approximately normal with mean 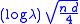 and variance 1. For a one-sided level
and variance 1. For a one-sided level  test with power
test with power 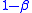 , the sample size required is
, the sample size required is

where and
and 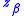 are the quantiles of the standard normal distribution.
are the quantiles of the standard normal distribution.
 and
and 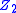 are the logrank statistics at two different time points in the same study (
are the logrank statistics at two different time points in the same study ( earlier). Again, assume the hazard functions in the two groups are proportional with hazard ratio
earlier). Again, assume the hazard functions in the two groups are proportional with hazard ratio  and
and 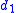 and
and  are the probabilities that a subject will have an event at the two time points where d1 ≤ d2.
are the probabilities that a subject will have an event at the two time points where d1 ≤ d2. 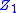 and
and  are approximately bivariate normal with means
are approximately bivariate normal with means  and
and 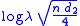 and correlation
and correlation  . Calculations involving the joint distribution are needed to correctly maintain the error rate when the data are examined multiple times within a study by a Data Monitoring Committee.
. Calculations involving the joint distribution are needed to correctly maintain the error rate when the data are examined multiple times within a study by a Data Monitoring Committee.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the logrank test is a hypothesis test to compare the survival
Survival analysis
Survival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
distributions of two samples. It is a nonparametric test and appropriate to use when the data are right skewed and censored
Censoring (statistics)
In statistics, engineering, and medical research, censoring occurs when the value of a measurement or observation is only partially known.For example, suppose a study is conducted to measure the impact of a drug on mortality. In such a study, it may be known that an individual's age at death is at...
(technically, the censoring must be non-informative). It is widely used in clinical trials to establish the efficacy of a new treatment compared to a control treatment when the measurement is the time to event (such as the time from initial treatment to a heart attack). The test is sometimes called the Mantel–Cox test, named after Nathan Mantel
Nathan Mantel
Nathan Mantel was a biostatistician best known for his work with William Haenszel which led to the Mantel–Haenszel test and its associated estimate, the Mantel–Haenszel odds ratio...
and David Cox. The logrank test can also be viewed as a time stratified Cochran–Mantel–Haenszel test
Cochran–Mantel–Haenszel statistics
In statistics, the Cochran–Mantel–Haenszel statistics are a collection of test statistics used in the analysis of stratified categorical data.. They are named after William G Cochran, Nathan Mantel and William Haenszel. One of these test statistics is the Cochran–Mantel–Haenszel test, which allows...
.
The test was first proposed by Nathan Mantel
Nathan Mantel
Nathan Mantel was a biostatistician best known for his work with William Haenszel which led to the Mantel–Haenszel test and its associated estimate, the Mantel–Haenszel odds ratio...
and was named the logrank test by Richard
Richard Peto
Sir Richard Peto FRS is Professor of Medical Statistics and Epidemiology at the University of Oxford.He attended Taunton's School in Southampton and subsequently studied Natural Sciences at Cambridge University....
and Julian Peto
Julian Peto
Julian Peto is an English statistician and cancer epidemiologist. He is Cancer Research UK Chair of Epidemiology at the London School of Hygiene and Tropical Medicine and the Institute of Cancer Research...
.
Definition
The logrank test statistic compares estimates of the hazard functions of the two groups at each observed event time. It is constructed by computing the observed and expected number of events in one of the groups at each observed event time and then adding these to obtain an overall summary across all time points where there is an event.Let j = 1, ..., J be the distinct times of observed events in either group. For each time
 , let
, let 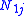 and
and  be the number of subjects "at risk" (have not yet had an event or been censored) at the start of period
be the number of subjects "at risk" (have not yet had an event or been censored) at the start of period 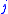 in the groups respectively. Let
in the groups respectively. Let  . Let
. Let 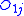 and
and  be the observed number of events in the groups respectively at time
be the observed number of events in the groups respectively at time 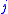 , and define
, and define 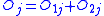 .
.Given that
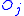 events happened across both groups at time
events happened across both groups at time 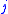 , under the null hypothesis (of the two groups having identical survival and hazard functions)
, under the null hypothesis (of the two groups having identical survival and hazard functions)  has the hypergeometric distribution with parameters
has the hypergeometric distribution with parameters 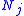 ,
,  , and
, and 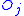 . This distribution has expected value
. This distribution has expected value 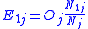 and variance
and variance 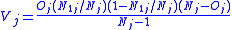 .
.The logrank statistic compares each
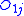 to its expectation
to its expectation  under the null hypothesis and is defined as
under the null hypothesis and is defined as
Asymptotic distribution
If the two groups have the same survival function, the logrank statistic is approximately standard normal. A one-sided level test will reject the null hypothesis if
test will reject the null hypothesis if  where
where  is the upper
is the upper  quantile of the standard normal distribution. If the hazard ratio is
quantile of the standard normal distribution. If the hazard ratio is  , there are
, there are  total subjects,
total subjects,  is the probability a subject in either group will eventually have an event (so that
is the probability a subject in either group will eventually have an event (so that 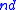 is the expected number of events at the time of the analysis), and the proportion of subjects randomized to each group is 50%, then the logrank statistic is approximately normal with mean
is the expected number of events at the time of the analysis), and the proportion of subjects randomized to each group is 50%, then the logrank statistic is approximately normal with mean 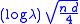 and variance 1. For a one-sided level
and variance 1. For a one-sided level  test with power
test with power 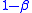 , the sample size required is
, the sample size required is
where
 and
and 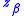 are the quantiles of the standard normal distribution.
are the quantiles of the standard normal distribution.Joint distribution
Suppose and
and 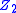 are the logrank statistics at two different time points in the same study (
are the logrank statistics at two different time points in the same study ( earlier). Again, assume the hazard functions in the two groups are proportional with hazard ratio
earlier). Again, assume the hazard functions in the two groups are proportional with hazard ratio  and
and 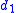 and
and  are the probabilities that a subject will have an event at the two time points where d1 ≤ d2.
are the probabilities that a subject will have an event at the two time points where d1 ≤ d2. 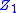 and
and  are approximately bivariate normal with means
are approximately bivariate normal with means  and
and 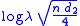 and correlation
and correlation  . Calculations involving the joint distribution are needed to correctly maintain the error rate when the data are examined multiple times within a study by a Data Monitoring Committee.
. Calculations involving the joint distribution are needed to correctly maintain the error rate when the data are examined multiple times within a study by a Data Monitoring Committee.Relationship to other statistics
- The logrank statistic can be derived as the score testScore testA score test is a statistical test of a simple null hypothesis that a parameter of interest \theta isequal to some particular value \theta_0. It is the most powerful test when the true value of \theta is close to \theta_0. The main advantage of the Score-test is that it does not require an...
for the Cox proportional hazards modelProportional hazards modelsProportional hazards models are a class of survival models in statistics. Survival models relate the time that passes before some event occurs to one or more covariates that may be associated with that quantity. In a proportional hazards model, the unique effect of a unit increase in a covariate...
comparing two groups. It is therefore asymptotically equivalent to the likelihood ratio test statistic based from that model.
- The logrank statistic is asymptotically equivalent to the likelihood ratio test statistic for any family of distributions with proportional hazard alternative. For example, if the data from the two samples have exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
s.
- If
 is the logrank statistic,
is the logrank statistic,  is the number of events observed, and
is the number of events observed, and 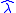 is the estimate of the hazard ratio, then
is the estimate of the hazard ratio, then 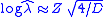 . This relationship is useful when two of the quantities are known (e.g. from a published article), but the third one is needed.
. This relationship is useful when two of the quantities are known (e.g. from a published article), but the third one is needed.
- The logrank statistic can be used when observations are censored. If censored observations are not present in the data then the Wilcoxon rank sum test is appropriate.
- The logrank statistic gives all calculations the same weight, regardless of the time at which an event occurs. The Peto logrank statistic gives more weight to earlier events when there are a large number of observations.

