
Proportional hazards models
Encyclopedia
Proportional hazards models are a class of survival models
in statistics. Survival models relate the time that passes before some event occurs to one or more covariate
s that may be associated
with that quantity. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed may double its hazard rate for failure. Other types of survival models such as accelerated failure time model
s do not exhibit proportional hazards. These models could describe a situation such as a drug that reduces a subject's immediate risk of having a stroke, but where there is no reduction in the hazard rate after one year for subjects who do not have a stroke in the first year of analysis.
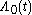 , describing how the hazard (risk) changes over time at baseline levels of covariates; and the effect parameters, describing how the hazard varies in response to explanatory covariates. A typical medical example would include covariates such as treatment assignment, as well as patient characteristics such as age, gender, and the presence of other diseases in order to reduce variability and/or control for confounding.
, describing how the hazard (risk) changes over time at baseline levels of covariates; and the effect parameters, describing how the hazard varies in response to explanatory covariates. A typical medical example would include covariates such as treatment assignment, as well as patient characteristics such as age, gender, and the presence of other diseases in order to reduce variability and/or control for confounding.
The proportional hazards condition states that covariates are multiplicatively related to the hazard. In the simplest case of stationary coefficients, for example, a treatment with a drug may, say, halve a subject's hazard at any given time , while the baseline hazard may vary. Note however, that the covariate
, while the baseline hazard may vary. Note however, that the covariate
is not restricted to binary predictors; in the case of a continuous covariate , the hazard responds logarithmically; each unit increase in
, the hazard responds logarithmically; each unit increase in  results in proportional scaling of the hazard. The Cox partial likelihood shown below, is obtained by using Breslow's estimate of the baseline hazard function, plugging it into the full likelihood and then observing that the result is a product of two factors. The first factor is the partial likelihood shown below, in which the baseline hazard has "canceled out". The second factor is free of the regression coefficients and depends on the data only through the censoring pattern. The effect of covariates estimated by any proportional hazards model can thus be reported as hazard ratio
results in proportional scaling of the hazard. The Cox partial likelihood shown below, is obtained by using Breslow's estimate of the baseline hazard function, plugging it into the full likelihood and then observing that the result is a product of two factors. The first factor is the partial likelihood shown below, in which the baseline hazard has "canceled out". The second factor is free of the regression coefficients and depends on the data only through the censoring pattern. The effect of covariates estimated by any proportional hazards model can thus be reported as hazard ratio
s.
Sir David Cox
observed that if the proportional hazards assumption holds (or, is assumed to hold) then it is possible to estimate the effect parameter(s) without any consideration of the hazard function. This approach to survival data is called application of the Cox proportional hazards model, sometimes abbreviated to Cox model or to proportional hazards model.
Survival analysis
Survival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
in statistics. Survival models relate the time that passes before some event occurs to one or more covariate
Covariate
In statistics, a covariate is a variable that is possibly predictive of the outcome under study. A covariate may be of direct interest or it may be a confounding or interacting variable....
s that may be associated
Association (statistics)
In statistics, an association is any relationship between two measured quantities that renders them statistically dependent. The term "association" refers broadly to any such relationship, whereas the narrower term "correlation" refers to a linear relationship between two quantities.There are many...
with that quantity. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed may double its hazard rate for failure. Other types of survival models such as accelerated failure time model
Accelerated failure time model
In the statistical area of survival analysis, an accelerated failure time model is a parametric model that provides an alternative to the commonly used proportional hazards models...
s do not exhibit proportional hazards. These models could describe a situation such as a drug that reduces a subject's immediate risk of having a stroke, but where there is no reduction in the hazard rate after one year for subjects who do not have a stroke in the first year of analysis.
Introduction
Survival models can be viewed as consisting of two parts: the underlying hazard function, often denoted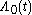 , describing how the hazard (risk) changes over time at baseline levels of covariates; and the effect parameters, describing how the hazard varies in response to explanatory covariates. A typical medical example would include covariates such as treatment assignment, as well as patient characteristics such as age, gender, and the presence of other diseases in order to reduce variability and/or control for confounding.
, describing how the hazard (risk) changes over time at baseline levels of covariates; and the effect parameters, describing how the hazard varies in response to explanatory covariates. A typical medical example would include covariates such as treatment assignment, as well as patient characteristics such as age, gender, and the presence of other diseases in order to reduce variability and/or control for confounding.The proportional hazards condition states that covariates are multiplicatively related to the hazard. In the simplest case of stationary coefficients, for example, a treatment with a drug may, say, halve a subject's hazard at any given time
 , while the baseline hazard may vary. Note however, that the covariate
, while the baseline hazard may vary. Note however, that the covariateCovariate
In statistics, a covariate is a variable that is possibly predictive of the outcome under study. A covariate may be of direct interest or it may be a confounding or interacting variable....
is not restricted to binary predictors; in the case of a continuous covariate
 , the hazard responds logarithmically; each unit increase in
, the hazard responds logarithmically; each unit increase in  results in proportional scaling of the hazard. The Cox partial likelihood shown below, is obtained by using Breslow's estimate of the baseline hazard function, plugging it into the full likelihood and then observing that the result is a product of two factors. The first factor is the partial likelihood shown below, in which the baseline hazard has "canceled out". The second factor is free of the regression coefficients and depends on the data only through the censoring pattern. The effect of covariates estimated by any proportional hazards model can thus be reported as hazard ratio
results in proportional scaling of the hazard. The Cox partial likelihood shown below, is obtained by using Breslow's estimate of the baseline hazard function, plugging it into the full likelihood and then observing that the result is a product of two factors. The first factor is the partial likelihood shown below, in which the baseline hazard has "canceled out". The second factor is free of the regression coefficients and depends on the data only through the censoring pattern. The effect of covariates estimated by any proportional hazards model can thus be reported as hazard ratioHazard ratio
In survival analysis, the hazard ratio is the ratio of the hazard rates corresponding to the conditions described by two sets of explanatory variables. For example, in a drug study, the treated population may die at twice the rate per unit time as the control population. The hazard ratio would be...
s.
Sir David Cox
David Cox (statistician)
Sir David Roxbee Cox FRS is a prominent British statistician.-Early years:Cox studied mathematics at St. John's College, Cambridge and obtained his PhD from the University of Leeds in 1949, advised by Henry Daniels and Bernard Welch.-Career:He was employed from 1944 to 1946 at the Royal Aircraft...
observed that if the proportional hazards assumption holds (or, is assumed to hold) then it is possible to estimate the effect parameter(s) without any consideration of the hazard function. This approach to survival data is called application of the Cox proportional hazards model, sometimes abbreviated to Cox model or to proportional hazards model.
The partial likelihood
Let Yi denote the observed time (either censoring time or event time) for subject i, and let Ci be the indicator that the time corresponds to an event (i.e. if Ci = 1 the event occurred and if Ci = 0 the time is a censoring time). The hazard function for the Cox proportional hazard model has the form-

This expression gives the hazard at time t for an individual with covariate vector (explanatory variables) X. Based on this hazard function, a partial likelihood can be constructed from the datasets as
-

where X1, ..., Xn are the covariate vectors for the n independently sampled individuals in the dataset (treated here as column vectors), and θj = exp(β′Xj).
The corresponding log partial likelihood is
-
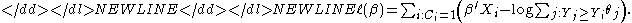
This function can be maximized over β to produce maximum partial likelihood estimates of the model parameters.
The partial score functionScore functionThe term score function may refer to:* Scoring rule, in decision theory, a measure of one's performance when making decisions under uncertainty* Score , the derivative of the log-likelihood function with respect to the parameter...
is
-

and the Hessian matrixHessian matrixIn mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of the partial log likelihood is
-

Using this score function and Hessian matrix, the partial likelihood can be maximized using the Newton-RaphsonNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
algorithm. The inverse of the Hessian matrix, evaluated at the estimate of β, can be used as an approximate variance-covariance matrix for the estimate, and used to produce approximate standard errorStandard errorStandard error can refer to:* Standard error , the estimated standard deviation or error of a series of measurements* Standard error stream, one of the standard streams in Unix-like operating systems...
s for the regression coefficients.
Tied times
Several approaches have been proposed to handle situations in which there are ties in the time data. Breslow's method describes the approach in which the procedure described above is used unmodified, even when ties are present. An alternative approach that is considered to give better results is Efron's method. Let tj denote the unique times, let Hj denote the set of indices i such that Yi = tj and Ci = 1, and let mj = |Hj|. Efron's approach maximizes the following partial likelihood.
-

The corresponding log partial likelihood is
-
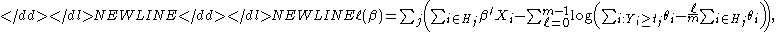
the score function is
-

and the Hessian matrix is
-

where
-

-

Note that when Hj is empty (all observations with time tj are censored), the summands in these expressions are treated as zero.
Time-varying predictors and coefficients
Extensions to time dependent variables, time dependent strata, and multiple events per subject, can be incorporated by the counting process formulation of Andersen and Gill.
In addition to allowing time-varying covariateTime-varying covariateA time-varying covariate is a term used in statistics, particularly in survival analyses. It reflects the phenomenon that a covariate is not necessarily constant through the whole study...
s (i.e., predictors), the Cox model may be generalized to time-varying coefficients as well. That is, the proportional effect of a treatment may vary with time; e.g. a drug may be very effective if administered within one month of morbidity, and become less effective as time goes on. The hypothesis of no change with time (stationarity) of the coefficient may then be tested. Details and software are available in Martinussen and Scheike (2006).
Specifying the baseline hazard function
The Cox model may be specialized if a reason exists to assume that the baseline hazard follows a particular form. In this case, the baseline hazard is replaced by a given function. For example, assuming the hazard function to be the Weibull hazard function gives the Weibull proportional hazards model.
is replaced by a given function. For example, assuming the hazard function to be the Weibull hazard function gives the Weibull proportional hazards model.
Incidentally, using the Weibull baseline hazard is the only circumstance under which the model satisfies both the proportional hazards, and accelerated failure timeAccelerated failure time modelIn the statistical area of survival analysis, an accelerated failure time model is a parametric model that provides an alternative to the commonly used proportional hazards models...
models.
The generic term parametric proportional hazards models can be used to describe proportional hazards models in which the hazard function is specified. The Cox proportional hazards model is sometimes called a semiparametric model by contrast.
Some authors (e.g. Bender, Augustin and Blettner) use the term Cox proportional hazards model even when specifying the underlying hazard function, to acknowledge the debt of the entire field to David Cox.
The term Cox regression model (omitting proportional hazards) is sometimes used to describe the extension of the Cox model to include time-dependent factors. However, this usage is potentially ambiguous since the Cox proportional hazards model can itself be described as a regression model.
Relationship to Poisson models
There is a relationship between proportional hazards models and Poisson regressionPoisson regressionIn statistics, Poisson regression is a form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown...
models which is sometimes used to fit approximate proportional hazards models in software for Poisson regression. The usual reason for doing this is that calculation is much quicker. This was more important in the days of slower computers but can still be useful for particularly large data sets or complex problems. Authors giving the mathematical details include Laird and Olivier (1981), who remark
"Note that we do not assume [the Poisson model] is true, but simply use it as a device for deriving the likelihood."
The book on generalized linear models by McCullagh and Nelder has a chapter on converting proportional hazards models to generalized linear modelGeneralized linear modelIn statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
s.
See also
- Survival analysisSurvival analysisSurvival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
- Weibull distribution
- Accelerated failure time modelAccelerated failure time modelIn the statistical area of survival analysis, an accelerated failure time model is a parametric model that provides an alternative to the commonly used proportional hazards models...
- Survival analysis
-
-
-
-
-
-
-
-
-
-

