Local asymptotic normality
Encyclopedia
In statistics
, local asymptotic normality is a property of a sequence of statistical model
s, which allows this sequence to be asymptotically approximated
by a normal location model, after a rescaling of the parameter. An important example when the local asymptotic normality holds is in the case of iid sampling from a regular parametric model.
The notion of local asymptotic normality was introduced by .
rn and Iθ and a random vector
such that, for every converging sequence ,
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, local asymptotic normality is a property of a sequence of statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
s, which allows this sequence to be asymptotically approximated
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
by a normal location model, after a rescaling of the parameter. An important example when the local asymptotic normality holds is in the case of iid sampling from a regular parametric model.
The notion of local asymptotic normality was introduced by .
Definition
A sequence of parametric statistical models } is said to be locally asymptotically normal (LAN) at θ if there exist matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
rn and Iθ and a random vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
such that, for every converging sequence ,
-
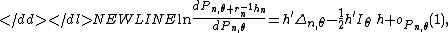
where the derivative here is a Radon–Nikodym derivative, which is a formalised version of the likelihood ratio, and where o is a type of big O in probability notationBig O in probability notationThe order in probability notation is used in probability theory and statistical theory in direct parallel to the big-O notation which is standard in mathematics...
. In other words, the local likelihood ratio must converge in distribution to a normal random variable whose mean is equal to minus one half the variance:-
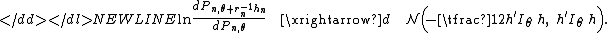
The sequences of distributions
and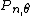 
are contiguousContiguity (probability theory)In probability theory, two sequences of probability measures are said to be contiguous if asymptotically they share the same support. Thus the notion of contiguity extends the concept of absolute continuity to the sequences of measures....
.
Example
The most straightforward example of a LAN model is an iid model whose likelihood is twice continuously differentiable. Suppose } is an iid sample, where each Xi has density function . The likelihood function of the model is equal to-
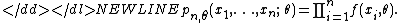
If f is twice continuously differentiable in θ, then-
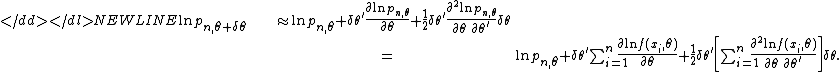
Plugging in , gives-
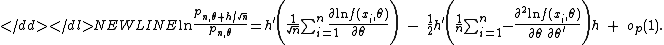
By the central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, the first term (in parentheses) converges in distribution to a normal random variable , whereas by the law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
the expression in second parentheses converges in probability to Iθ, which is the Fisher information matrix:-
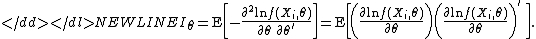
Thus, the definition of the local asymptotic normality is satisfied, and we have confirmed that the parametric model with iid observations and twice continuously differentiable likelihood has the LAN property.
-
-
-
-
-